分析技术研习室

Logo

课题组每周研讨会

View the Project on GitHub XSLiuLab/Workshop

生存分析

资料

图书：生存分析应用

小抄：survminer

R包：

介绍

生存分析就是对直到某一事件发生所经历的时间(生存时间)进行建模

生存分析主要的应用：

生存分析最重要的三个函数是：生存函数，风险函数

特征：删失，时间

主要的方法：

两个函数

生存函数：个体存活到某个时间点t的概率，或者说到时间t为止，感兴趣的事件(T)没有发生的概率: \(S(t)=pr(T>t),0<t<\infty\) 风险函数：个体存活到某个时间点t，但是在接下来一个小的时间间隔后死亡的概率除以这个时间间隔的长度也就是瞬时死亡率： \(h(t)=\lim\limits_{\delta\rightarrow0}\frac{pr(t<T<t+\delta|T>t)}{\delta}\)

方法

参数法

先假设生存时间服从某些分布，再估计这些分布的参数

主要有指数分布和weibull分布

非参数法

Kaplan-Meier estimator

非参数法最常用的是KM估计(Kaplan-Meier estimator)

条件概率：

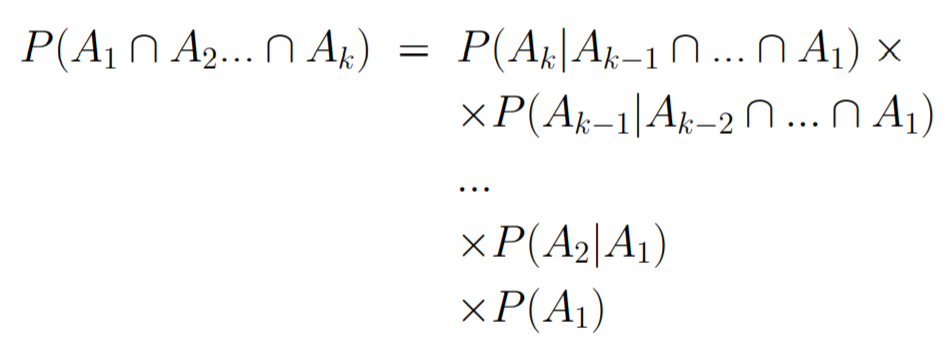
KM估计算的是条件概率：

对于这样的区间有这些情况：

所以KM法估计的生存函数就是：

算法：

tt <- c(7,6,6,5,2,4)
cens <- c(0,1,0,0,1,1)
result.km <- survfit(Surv(tt, cens) ~ 1)
summary(result.km)

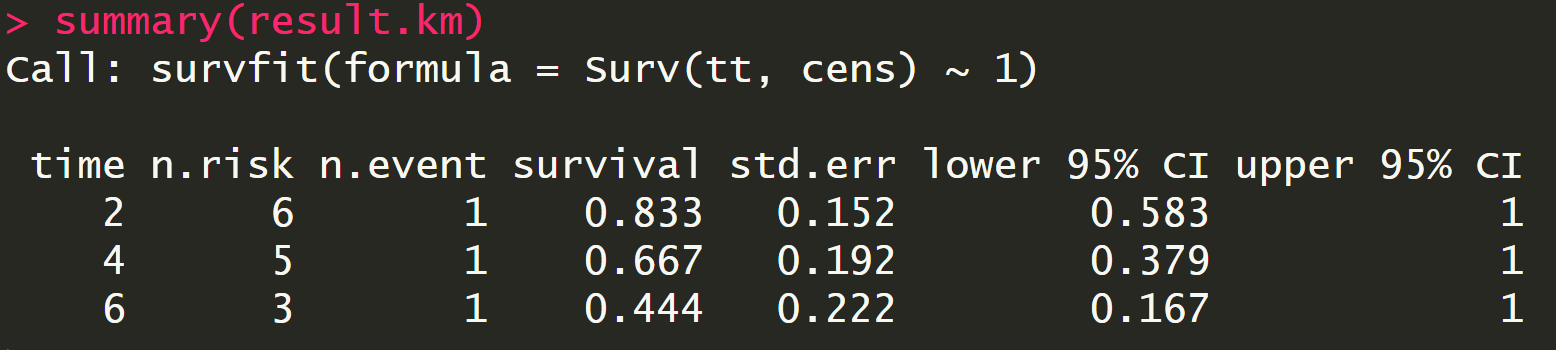
置信区间的估计

在估计方差前要了解一下delta method:如果一个随机变量有均值$\mu$和方差$\sigma^2$ ,那么对于足够大的样本g(x)就有近似的均值$g(\mu)$和方差$\sigma^2[g’(\mu)]^2$

然后就可以使用这个方法估计方差：

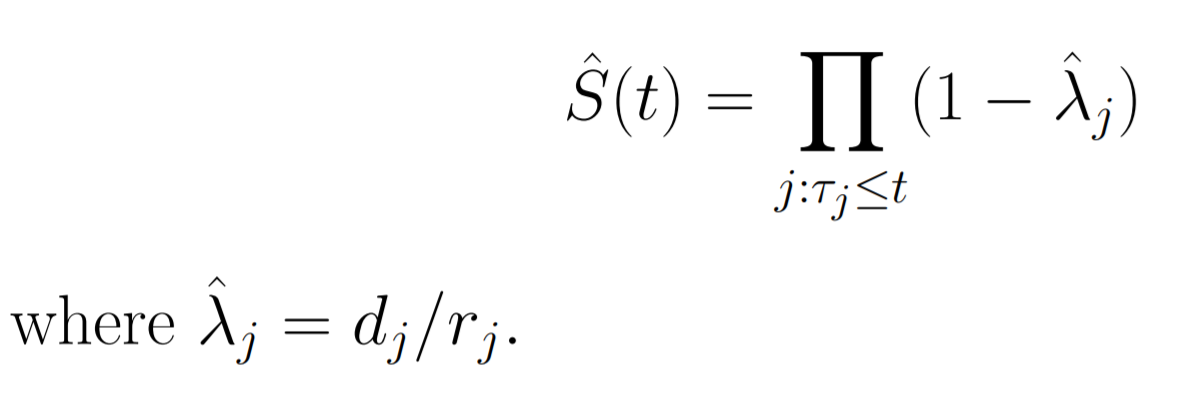
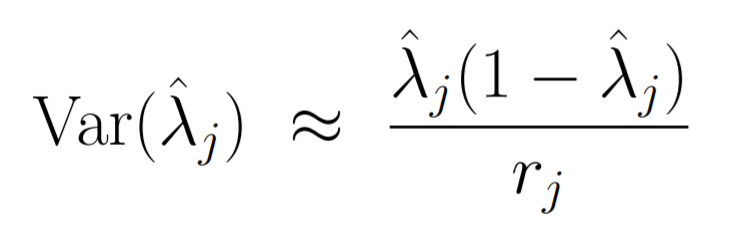
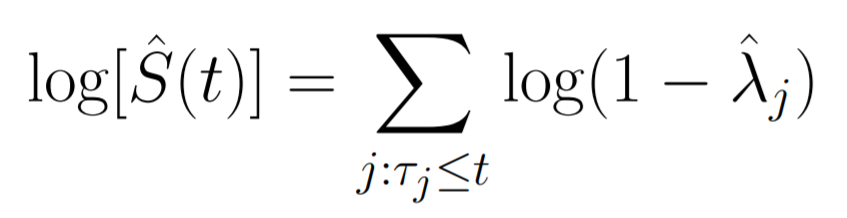
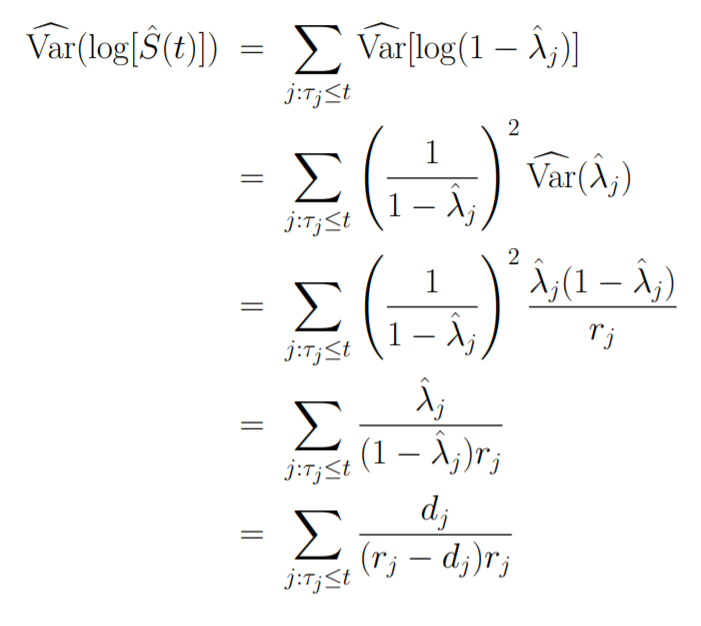
再次使用delta method：

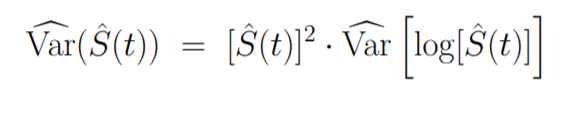
但是基于这个方差算出来的置信区间可能大于1或者小于0，一个更好的方法是对log(-logS(t))估计置信区间：

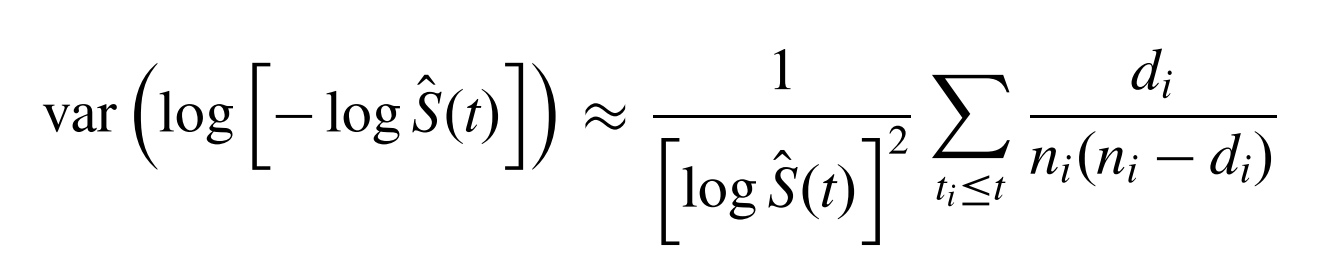
在survfit函数中加入conf.type参数就可以指定log-log方法

result.km <- survfit(Surv(tt, cens) ~ 1, conf.type="log-log")
plot(result.km)

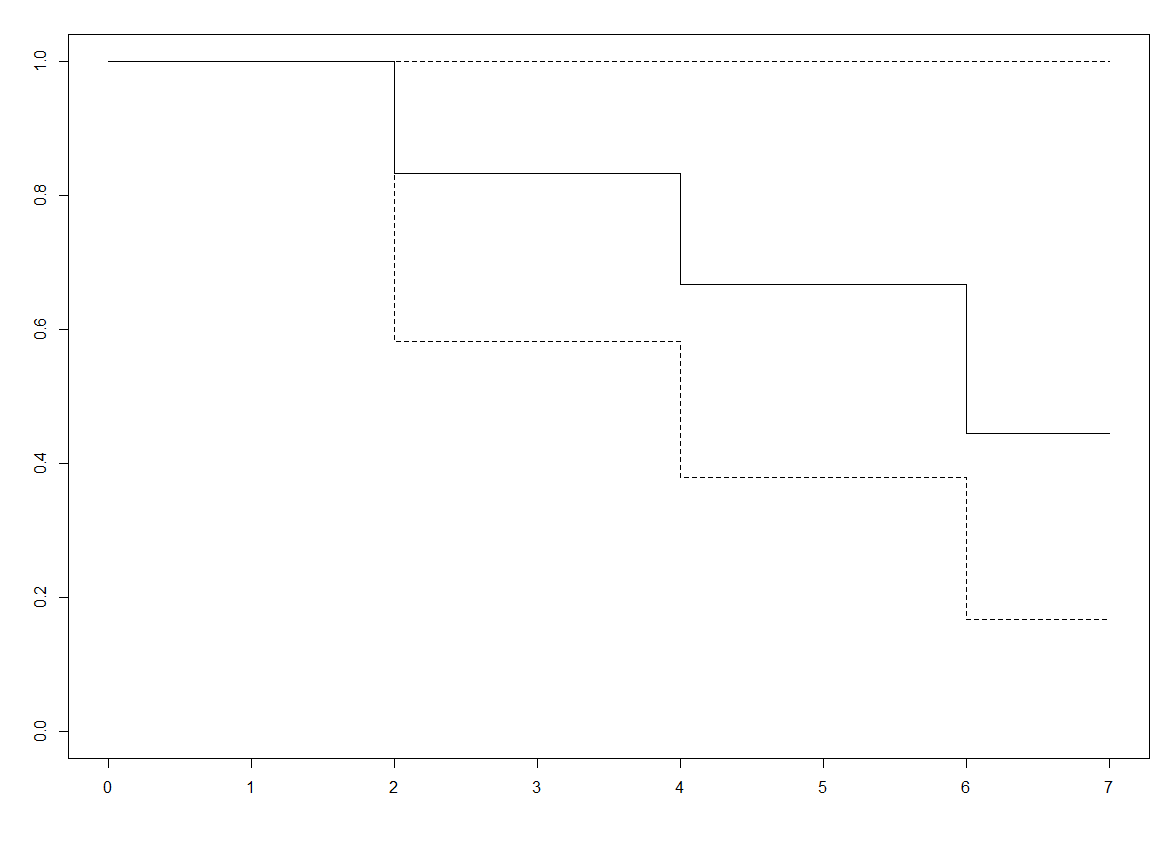
log-rank比较两组生存时间的差异

原假设是：$H_0:S_1(t)=S_0(t)$ S1和S0分别表示实验组和对照组的生存分布

备择假设是使用Lehman alternative：$H_A：S_1(t)=[S_o(t)]^\psi$ 也可以表示成：$h_1(t)=\psi h_0(t)$

所以我们也可以将假设检验改为： \(H_0:\psi =1 \\ H_A:\psi <1\) 接下来构建统计量：

对失败时间进行排序，对每个失败的时间都可以得到下面的二联表：

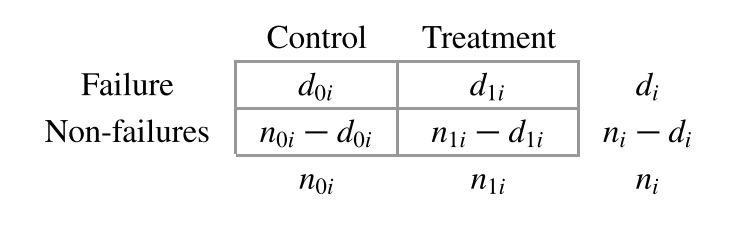
如果我们假设实验组和对照组没有差异，固定$n_{0i},n_{1i},d_i$ 那么 $d_{0i}$ 服从超几何分布(可以理解为一个盒子里有$n_{0i}$ 个蓝色的球，$n_{1i}$个红色的球，不返回的抽取$d_i$个球，如果抽到红色和蓝色的球的概率是一样的，那么抽到的蓝色的球服从超几何分布）

期望和方差分别为： \(e_{0i}=E(d_{0i})=\frac{n_{0i}d_i}{n_i} \\ v_{0i}=var(d_{0i})=\frac{n_{0i}n_{1i}d_i(n_i-d_i)}{n_i^2(n_i-1)}\) 然后把所有的失败时间的表的观察到的$d_{0i}$与其期望的差加起来得到一个统计量$U_0$ ,将所有的方差加起来得到$V_0$ ,之后，就可以得到一个服从正态分布或者卡方分布的统计量： \(U_0=\sum_{i=1}^N(d_{0i}-e_{0i})=\sum d_{0i}-\sum e_{0i}\\ V_0=\sum v_{0i}\\ \\ \frac{U_0}{\sqrt{V_0}}\sim N(0,1)\\ \frac{U_0^2}{V_0}\sim \chi_1^2\) 然后就可以算p值了，当我们需要比较大于2组的的时候，实际上是在cox回归中通过score test来检验这个变量的回归系数

也可以将这种检验进行推广，给他加上一个权重，weighted log-rank test：

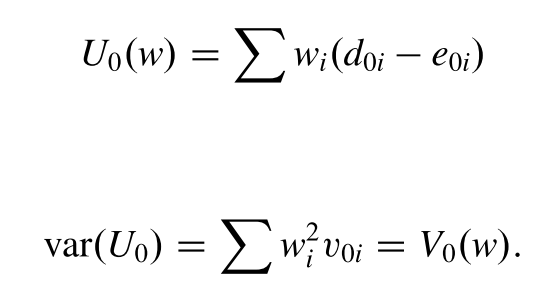
权重的确定可以把两组样本混合，然后计算Kaplan-Meier estimator得到：

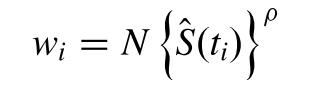
这种检验也叫做Fleming-Harrington G(ρ) test，ρ=0的时候就是log-rank test，这种方法给早期的生存差异一个较大的权重

在R中可以直接用survdiff()来计算不同组的差异，这个函数的参数rho就是上面的权重中的ρ

##胰腺癌的二期临床数据
head(pancreatic)
  stage    onstudy progression      death
1     M 12/16/2005    2/2/2006 10/19/2006
2     M   1/6/2006   2/26/2006  4/19/2006
3    LA   2/3/2006    8/2/2006  1/19/2007
4     M  3/30/2006           .  5/11/2006
5    LA  4/27/2006   3/11/2007  5/29/2007
6     M   5/7/2006   6/25/2006 10/11/2006

library(asaur)
library(date)
library(survival)
head(pancreatic)
attach ( pancreatic )
Progression_d <- as.date(as.character(progression))
OnStudy_d <- as.date(as.character(onstudy))
Death_d <- as.date(as.character(death))
# compute progression free survival
progressionOnly <- Progression_d-OnStudy_d
overallSurvival <- Death_d-OnStudy_d
pfs <- pmin(progressionOnly , overallSurvival)
pfs[is.na(pfs)] <- overallSurvival[is.na(pfs)]

pfs_month <- pfs/30.5

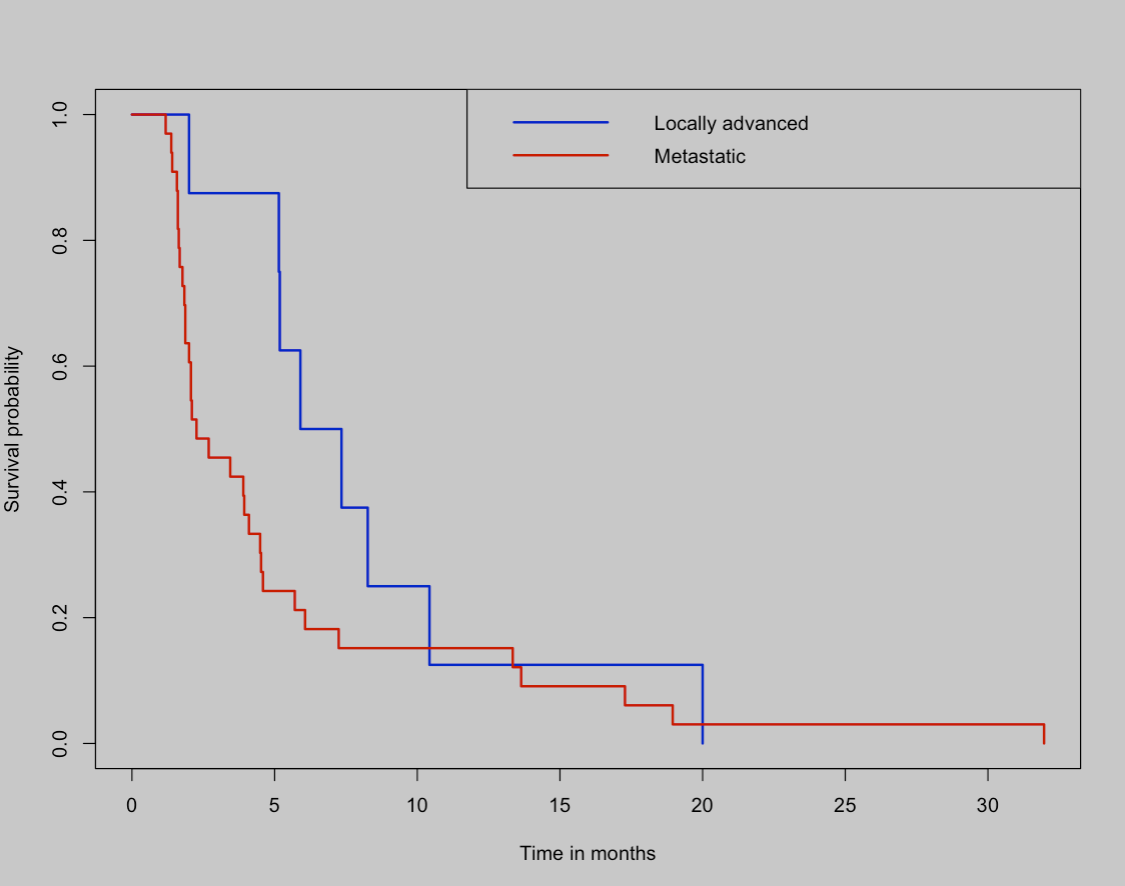
plot(survfit(Surv(pfs_month) ~ stage), xlab="Time in months", ylab="Survival probability",
     col=c("blue", "red"), lwd=2)
legend("topright", legend=c("Locally advanced", "Metastatic"),
       col=c("blue","red") , lwd=2)

##log-rank
survdiff(Surv(pfs) ~ stage, rho=0)
survdiff(Surv(pfs) ~ stage, rho=1)

image-20200602105500615

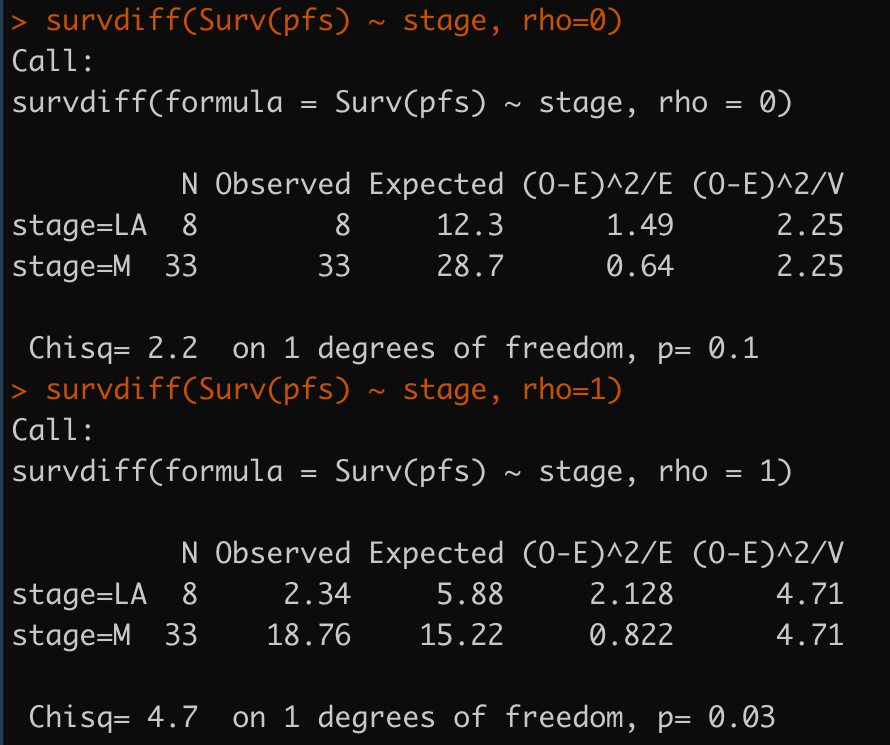
image-20200602105737602

cox比例风险回归

首先定义一个风险比率：$\psi_i = e^{z_i\beta}$ ,$z_i$是协变量的值，β是系数，一个协变量一个系数: \(h_i(t_j)=h_0(t_j)\psi_i ,\psi_i = e^{z_i\beta}\) 进行Log转化得到： \(log(h_i(t_j))=log(h_0(t_j))+\beta_1z_1+\beta_2z_2+...\beta_px_p\) 这个就是cox风险比例回归模型,

对于时间t1，我们可以计算病人i失败的概率： \(p1=\frac{h_i(t1)}{\sum_{k \in R_i}h_k(t_1)}=\frac{h_0(t_1)\psi_i}{\sum_{k\in R_1}h_0(t_1)\psi_k}=\frac{\psi_i}{\sum_{k \in R_i}\psi_k}\) 然后对于每一个时间(改变R，丢弃死亡的和缺失的数据)都可以算p，得到partial likelihood： \(L(\psi)=p_1p_2...p_D\) 可以通过最大似然估计来计算系数β

然后就可以对系数进行检验，主要有三种检验Wald test, score test, likelihood ratio test

首先我们需要从log的似然函数中得到两个函数：

一个是分数函数 :是log似然函数的一阶导数：$S(\beta)=l’(\beta)$

第二个是信息函数：是log似然函数的二阶导数：$I(\beta)=-S’(\beta)=-l’’(\beta)$

The Wald Test

可以构建一个Z统计量：$\hat{\beta}/s.e.(\hat{\beta})$ ,可以用$1/I(\hat{\beta})$来估计$\hat{\beta}$的方差，标准误为：$s.e.(\hat{\beta})=1/\sqrt{I(\hat{\beta})}$

使用这个统计量来计算p值或者构建置信区间

The Score Test

score统计量为$Z_s=S(\beta=0)/\sqrt{I(\beta=0)}$ 如果$ Z_S >z_{\alpha/2}$ 的时候拒绝原假设$\beta=0$

这种方法不需要进行最大似然估计的

The Likelihood Ratio Test

这个检验来自统计学原理：

$2[l(\beta=\hat{\beta})-l(\beta=0)]$ 近似服从自由度为1的卡方分布

在R里面可以使用coxph来进行cox回归分析

Survival analysis in R

用的包是survival包，示例数据是包内置数据集lung

?lung

主要用到的函数包括：

Surv() 输入的是时间和状态(死亡或者删失)，返回的结果是一个特殊的向量，对应的是每个时间发生的事件，用+表示删失：

s <- Surv(lung$time, lung$status)
head(s)
#[1]  306   455  1010+  210   883  1022+

接下来就可以用survfit()来拟合生存曲线：

sfit <- survfit(Surv(time, status)~1, data=lung)##不分组
sfit1 <- survfit(Surv(time, status)~sex, data=lung)##按性别分组

summary(sfit1)
summary(sfit1, times=seq(0, 1000, 100))##规定时间段

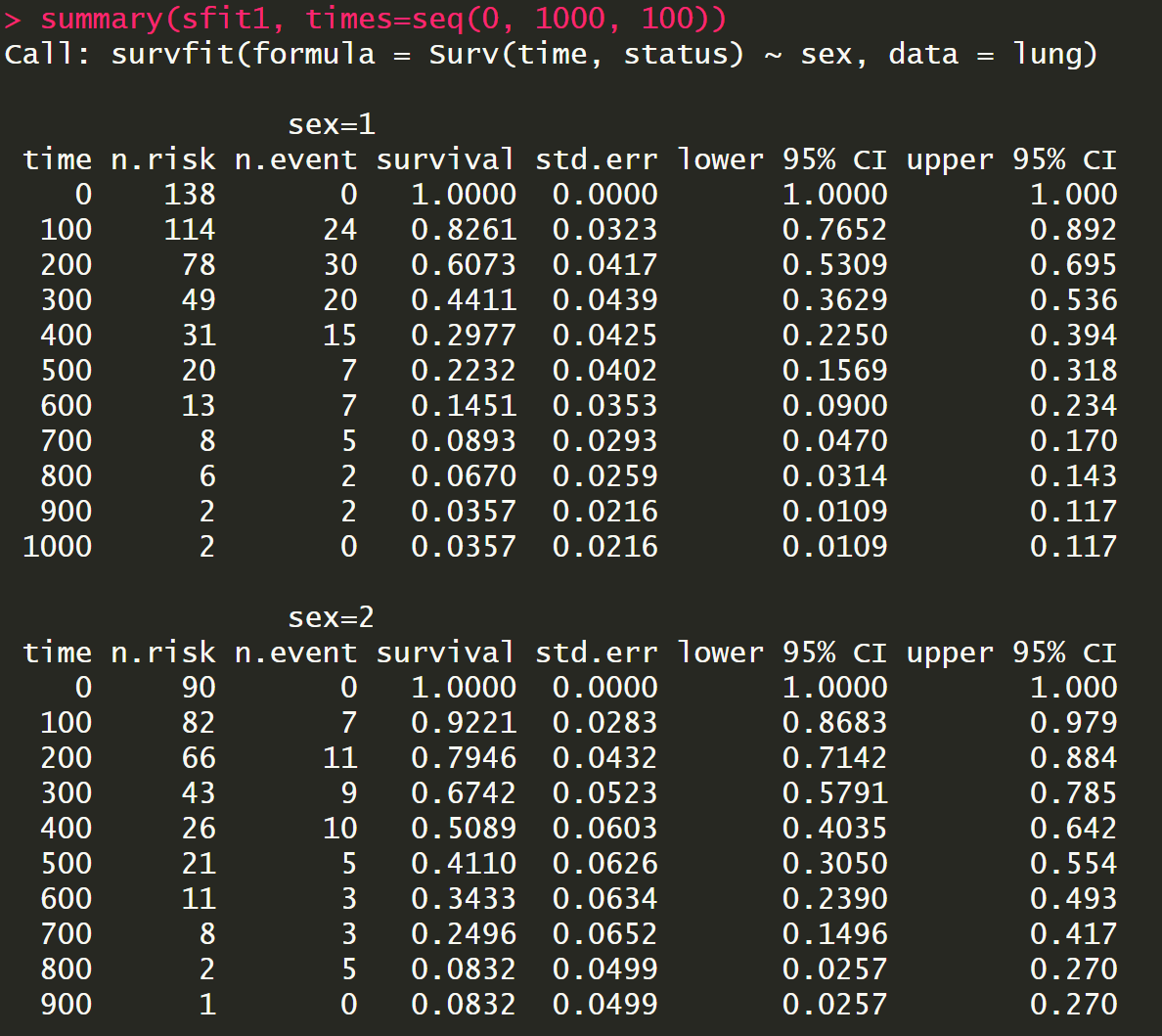
可以直接用plot来画图，也可以用survminer包中的ggsurvplot函数来画生存曲线图：

plot(sfit1)

library(survminer)
ggsurvplot(sfit1)

ggsurvplot(sfit1, conf.int=TRUE, pval=TRUE, risk.table=TRUE, 
           legend.labs=c("Male", "Female"), legend.title="Sex",  
           palette=c("dodgerblue2", "orchid2"), 
           title="Kaplan-Meier Curve for Lung Cancer Survival", 
           risk.table.height=.15)

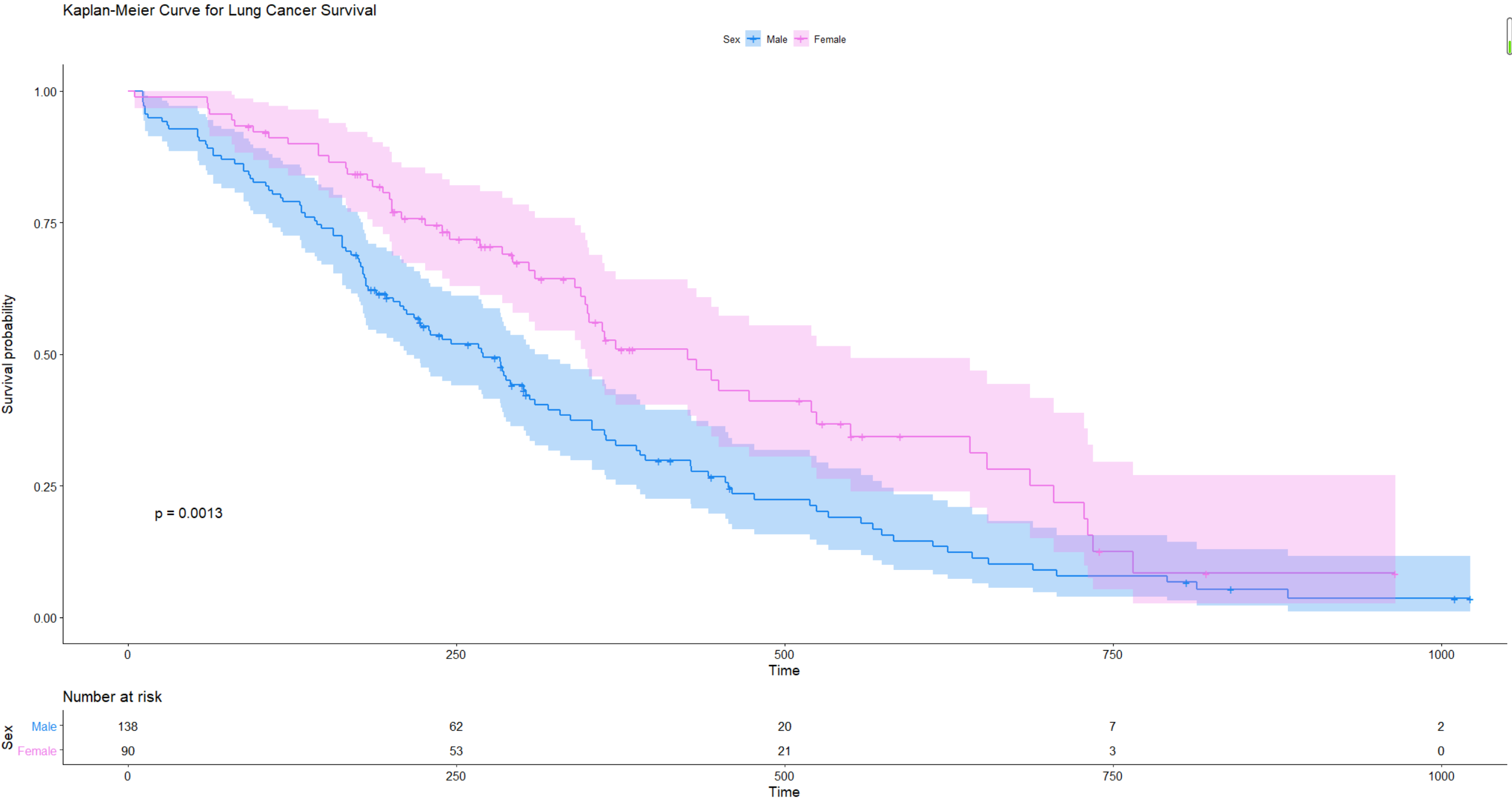
图里面的p值是通过log-rank 检验计算的，也可以用survdiff来得到：

survdiff(Surv(time, status)~sex, data=lung)

进一步还可以用coxph()检测多个变量对生存的影响,这个函数输入的自变量是想要检查的变量，因变量是Surv()生成的对象：

fit <- coxph(Surv(time, status)~sex+age+ph.ecog+ph.karno+pat.karno+meal.cal+wt.loss, data=lung)
fit
summary(fit)

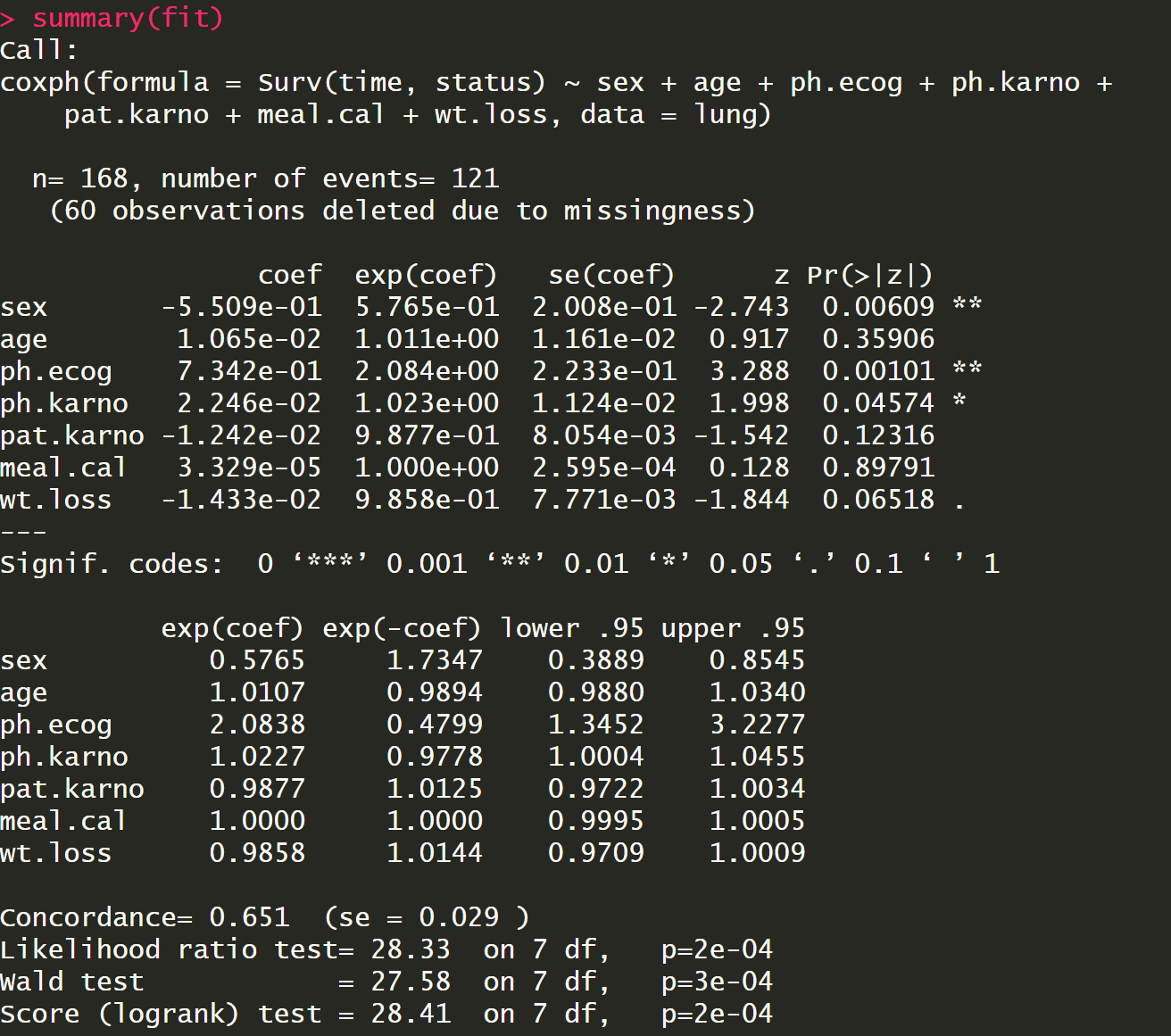
结果里面的第一列coef就是系数β，第二列exp(coef)就是$e^\beta$ 也就是风险比率(hazard ratio,HR)，HR等于1没有效应，大于1表示风险增大，小于1风险减少，比如性别有男性和女性，以男性为基准，从男性到女性生存风险大概降低40%

可以通过逐步回归找到”有用”的变量：

fit <- coxph(Surv(time, status)~sex+age+ph.ecog+ph.karno+pat.karno+meal.cal+wt.loss, 
             data=na.omit(lung))
stepwise <- step(fit,scope = list(upper=~sex+age+ph.ecog+ph.karno+pat.karno+meal.cal+wt.loss,
                                  lower=~sex))
stepwise

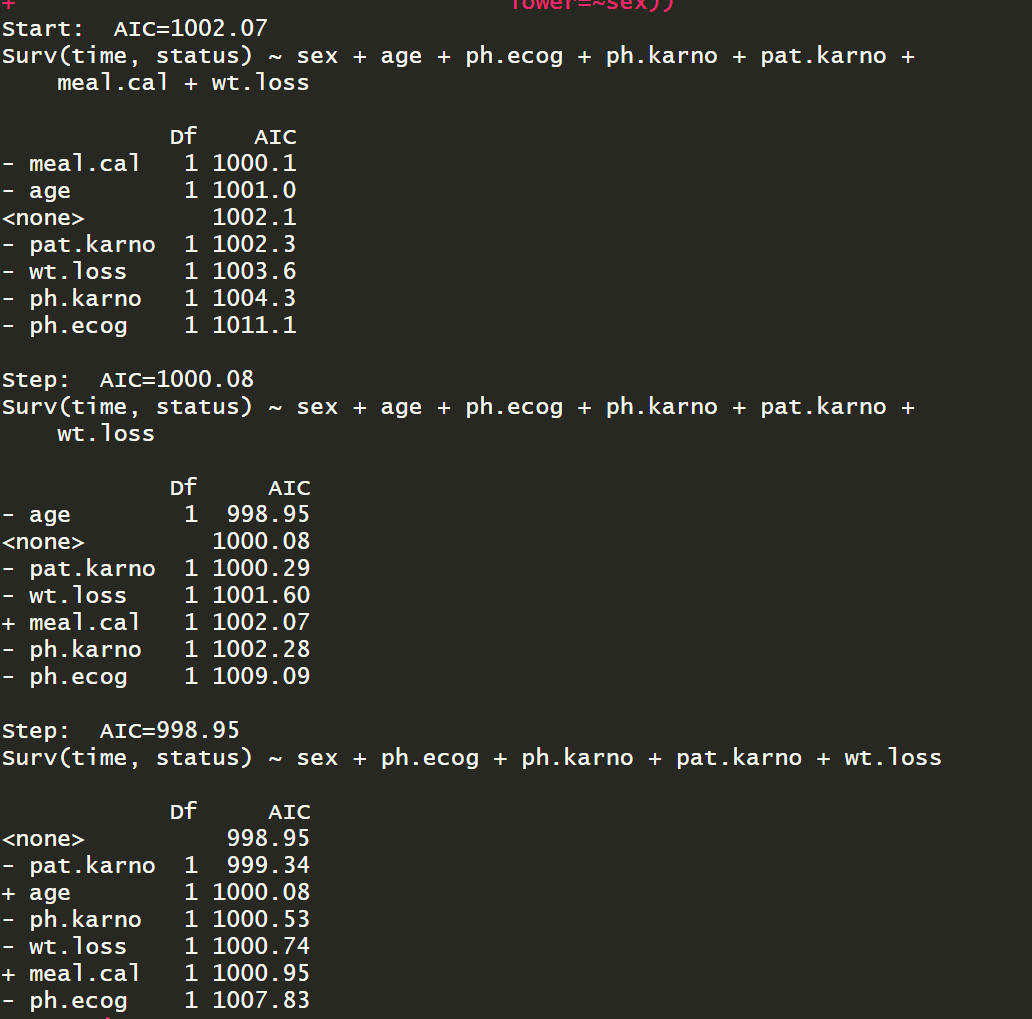
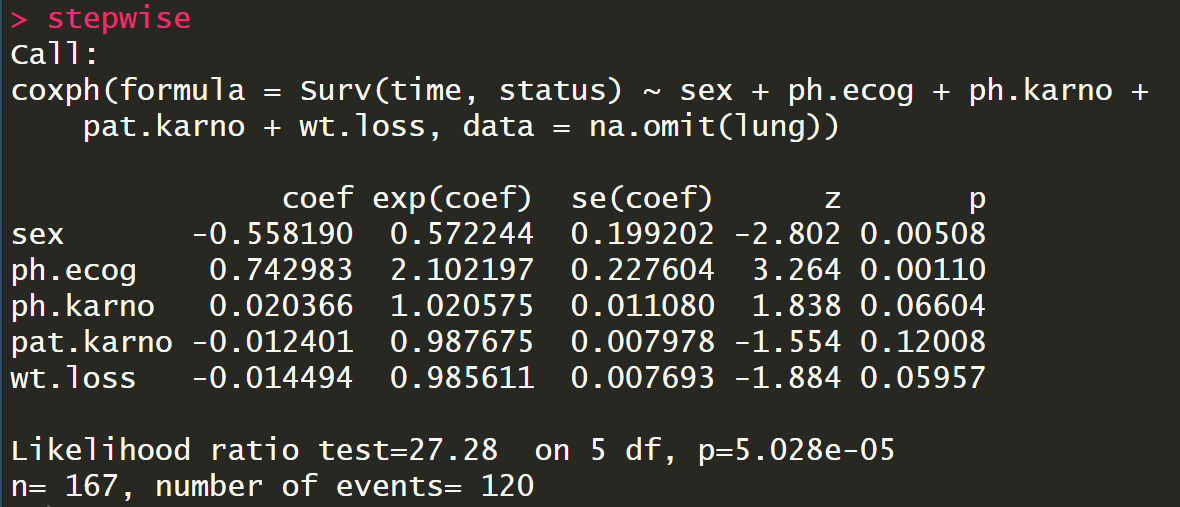
AIC叫做赤池信息准则，是当使用似然函数作为目标函数计算模型参数时，衡量模型拟合优良性的一个标准：

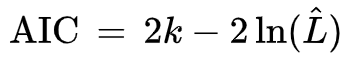
k是模型参数，L是似然函数，从一组可供选择的模型中选择最佳模型时，通常选择AIC最小的模型

然后可以通过森林图来可视化cox回归的结果：

ggforest(fit3,data = lung)