分析技术研习室
课题组每周研讨会
第十期:聚类
- 资料:R 聚类图书
聚类分析的思想:对于有p个变量的数据集来说,每个观测值都是p维空间中的一个点,所以属于同一类的点在空间中的距离应该显著小于属于不同类的点之间的距离
聚类距离测度
1.欧氏(Euclidean)距离: \(d_{euc}(x, y)=\sqrt{\sum_{i=1}^{n}(x_i-y_i)^2}\) 2.曼哈顿(Manhattan)距离: \(d_{man}(x,y)=\sum_{i=1}^{n}|(x_i-y_i)|\) x,y都是n维的向量
还有一些不相似性度量也可以来表示距离:
3.Pearson线性相关距离:也就是1减去Pearson相关系数,Pearson相关是衡量两个变量的线性相关性的,对数据的假设:Pearson相关系数应用于连续变量,假定两组变量均为正态分布、存在线性关系且等方差 \(d_{cor}(x,y)=1-\frac{\sum_{i=1}^{n}(x_i-\bar{x})(y_i-\bar{y})}{\sqrt{\sum_{i=1}^{n}(x_i-\bar{x})^2\sum_{i=1}^{n}(y_i-\bar{y})^2}}\) 4.cosine相关距离:是Pearson相关的一个特例,就是将$\bar{x}$和$\bar{y}$用0代替 \(d_{cos}(x,y)=1-\frac{|\sum_{i=1}^nx_iy_i|}{\sqrt{\sum_{i=1}^nx_i^2\sum_{i=1}^ny_i^2}}\) 5.Spearman相关距离:spearman相关计算的是变量秩之间的相关性,也是1减去Spearman相关系数 \(d_{spear}(x,y)=1-\frac{\sum_{i=1}^{n}(x_i’-\bar{x’})(y_i’-\bar{y’})}{\sqrt{\sum_{i=1}^{n}(x_i’-\bar{x’})^2\sum_{i=1}^{n}(y_i’-\bar{y’})^2}}\) $x_i’,y_i’$ 是$x_i,y_i$的秩
6.Kendall 相关距离:
Kendall相关方法是衡量变量秩的correspondence
对于大小是n的变量x和y,可能的匹配对数是$\frac{n(n-1)}{2}$ ;首先按照x对xy对进行排序,如果xy是相关的,x和y应该有一样的秩序;对于每个$y_i$计算大于$y_i$的y数量(concordant pairs (c))和小于$y_i$的y数量(discordant pairs (d)): \(d_{kend}(x,y)=1-\frac{n_c-n_d}{\frac{1}{2}n(n-1)}\) $n_c$是concordant pairs的总数量,$n_d$是discordant pairs的总数量
距离的选择
如果我们关注的是变量的变化趋势而不是变量的具体的值的时候,比如基因的表达,我们就可以使用基于相关性的距离测度,另外要注意的是pearson相关对outliers比较敏感,这个时候可以使用spearman相关
当我们关注的是变量的值的大小,可以使用欧氏距离来聚类
数据标准化
当变量是由不同的标度测量的时候,最好要对数据进行标准化使之可以进行比较;一般情况在下对变量进行缩放使之:标准差是1,均值是0;当变量的均值或者标准差相差较大的时候也可以对数据进行scale:
\(\frac{x_i-center(x)}{scale(x)}\)
center(x)可以是均值或者中位数;scale(x)可以是标准差,四分位间距,或者绝对中位差(median absolute deviation,MAD),R里面可以使用scale() 函数进行标准化
MAD的定义:数据点到中位数的绝对偏差的中位数
$MAD=median( X_i-median(X) )$
计算距离矩阵
使用的数据集为USArrests:
df <- USArrests
df_scaled <- scale(df)##标准化
计算距离的R函数有很多,如:
dist()get_dist()factoextra包里面的,可以计算基于相关性的距离,包括“pearson”, “kendall” “spearman”daisy()cluster包里面的,可以处理除了数值变量以外的其他变量类型(如分类变量,定序变量等)
注意:这些计算距离的函数都是计算行之间的距离,所以如果我们要计算变量(列)之间的距离,先要将其转置
dist.eucl <- dist(df_scaled,method = "euclidean")##欧氏距离
class(dist.eucl)#[1] "dist"
as.matrix(dist.eucl)[1:3,1:3]
# Alabama Alaska Arizona
# Alabama 0.000000 2.703754 2.293520
# Alaska 2.703754 0.000000 2.700643
# Arizona 2.293520 2.700643 0.000000
library(factoextra)
dist_cor <- get_dist(df_scaled,method = "pearson")##相关性距离
as.matrix(dist_cor)[1:3,1:3]
# Alabama Alaska Arizona
# Alabama 0.0000000 0.7138308 1.4465948
# Alaska 0.7138308 0.0000000 0.8307246
# Arizona 1.4465948 0.8307246 0.0000000
library(cluster)
data("flower")
head(flower,3)
# V1 V2 V3 V4 V5 V6 V7 V8
# 1 0 1 1 4 3 15 25 15
# 2 1 0 0 2 1 3 150 50
# 3 0 1 0 3 3 1 150 50
str(flower)
# 'data.frame': 18 obs. of 8 variables:
# $ V1: Factor w/ 2 levels "0","1": 1 2 1 1 1 1 1 1 2 2 ...
# $ V2: Factor w/ 2 levels "0","1": 2 1 2 1 2 2 1 1 2 2 ...
# $ V3: Factor w/ 2 levels "0","1": 2 1 1 2 1 1 1 2 1 1 ...
# $ V4: Factor w/ 5 levels "1","2","3","4",..: 4 2 3 4 5 4 4 2 3 5 ...
# $ V5: Ord.factor w/ 3 levels "1"<"2"<"3": 3 1 3 2 2 3 3 2 1 2 ...
# $ V6: Ord.factor w/ 18 levels "1"<"2"<"3"<"4"<..: 15 3 1 16 2 12 13 7 4 14 ...
# $ V7: num 25 150 150 125 20 50 40 100 25 100 ...
# $ V8: num 15 50 50 50 15 40 20 15 15 60 ...
dd <- daisy(flower)##计算含有分类变量,定序变量的距离
as.matrix(dd)[1:3,1:3]
# 1 2 3
# 1 0.0000000 0.8875408 0.5272467
# 2 0.8875408 0.0000000 0.5147059
# 3 0.5272467 0.5147059 0.0000000
划分聚类(Partitioning clustering)
划分聚类需要我们指定类别的数量
最常用的有:
- K-mean聚类
- K-medoids clustering (PAM)
- CLARA algorithm
K均值聚类
k表示我们想要数据聚成的类数,最终的结果是实现高的类内相似性和低的类间相似性 \(W(C_k)=\sum_{xi\in C_k}(x_i-\mu_k)^2\) $x_i$是属于$C_k$类的数据点,$\mu_k$是$C_k$类的中心点,也就是属于$C_k$类的所有数据点的均值,所以$W(C_k)$表示了类内的variation,定义总的within-cluster variation为: \(tot.withiness=\sum^k_{k=1}W(C_k)=\sum^k_{k=1}\sum_{xi\in C_k}(x_i-\mu_k)^2\) 我们的目的就是使上式最小化
算法
- 确定类的数目k
- 随机选取k个点作为起始聚类中心(initial cluster centers)
- 将每个观测值分配到最近的中心点(欧氏距离)
- 更新聚类中心:计算每个类的数据点的平均值作为新的聚类中心
- 迭代3,4步,直到聚类状态不再变化或者达到最大的迭代数目(R中默认是10)
R
kmeans(x, centers, iter.max = 10, nstart = 1)
- x: 数值矩阵,数据框或者数值向量
- centers: 类数或者起始的距离中心,如果输入的是一个数值的话则随机选取x的行作为初始聚类中心
- iter.max: 迭代的最大次数
- nstart: 开始选择随机聚类中心的次数,比如nstart=5,则是开始随机选择5次k个聚类中心,最后选择结果最好的
如何选择最佳聚类数?
一个简单的方法就是尝试不同的聚类数目k,计算上面的total within sum of square;随着聚类数目的增加WSS的趋势一定会下降(最极端的情况就是每个点都是一个类),当k小于真实聚类数时WSS下降幅度会很大,而当k大于真实聚类数时,再增加k WSS的下降幅度会骤减,所以会存在一个拐点
library(factoextra)
fviz_nbclust(df_scaled,kmeans,method = "wss")+
geom_vline(xintercept = 4,linetype=2)
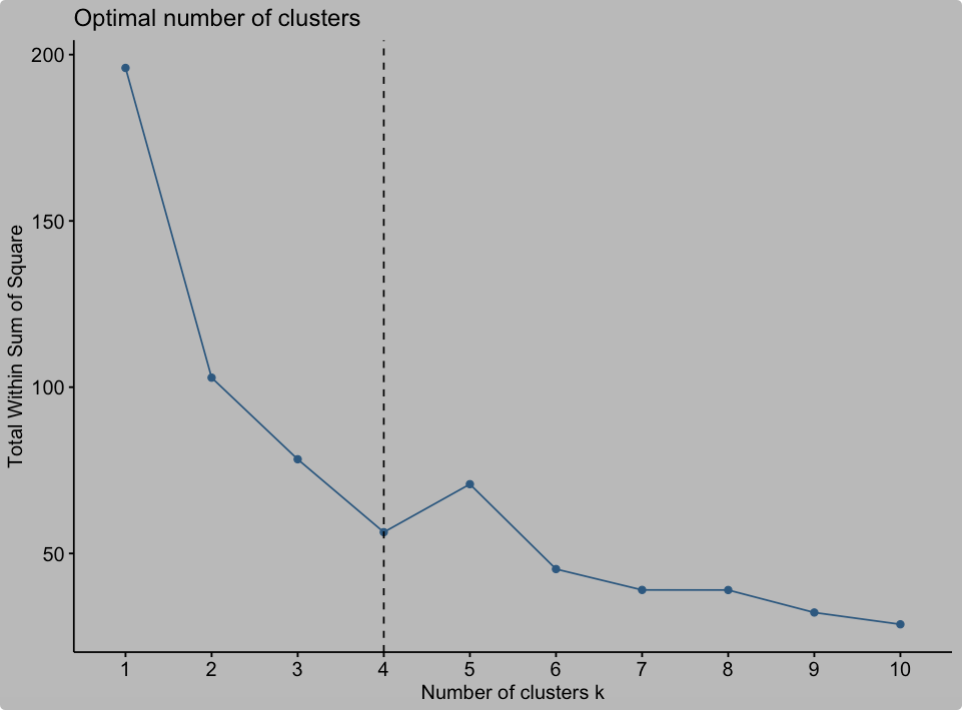
最佳聚类数为4:
set.seed(2020720)
km_res <- kmeans(df_scaled,4,nstart = 25)
print(km_res)
names(km_res)
# [1] "cluster" "centers" "totss" "withinss" "tot.withinss"
# [6] "betweenss" "size" "iter" "ifault"
结果包括聚类的中心点,每个观测值所属的类,wss
对于高维的数据我们可以先降维再可视化聚类的结果:
fviz_cluster(km_res, data = df_scaled)

K-Medoids
在k-medoids聚类中每个类由类内的某个点来代替,这些点就叫聚类中心(cluster medoids)
在 K-means 算法中,我们每次选簇的平均值作为新的中心,迭代直到簇中对象分布不再变化。因此一个具有很大极端值的对象会扭曲数据分布,造成算法对极端值敏感; K-Medoids算法不选用平均值而是用中心点作为参照点
最常用的k-medoids聚类方法是PAM算法(Partitioning Around Medoids)
PAM 算法
- 随机选择k个点作为medoids(或者指定k个点)
- 按照距离最佳,将剩余的点分配到最近的中心点
- 在每一类里面,对除初始的medoids点外的所有其他点,按顺序计算当其为新的medoids时准则函数的值是否下降,选择使其下降最多的点作为新的中心点(准则函数为所有点到其最近中心点的距离的和)
- 迭代3,4直到准则函数不再下降(medoids不再变化)
R
cluster::pam(x, k, metric = "euclidean", stand = FALSE)
- x : 可以是数值矩阵或者数据框,行是观测,列是变量;也可以是距离矩阵
- k : 类数
- metric : 计算距离的方法,可以是euclidean或者manhattan
- stand: 逻辑值,输入的列是否要标准化
首先需要估计最佳聚类数,可以使用平均轮廓法(average silhouette method),平均轮廓值越高说明聚类质量越好
可以使用factoextra 包中的fviz_nbclust函数来计算:
fviz_nbclust(df_scaled,pam,method = "silhouette")+
theme_classic()
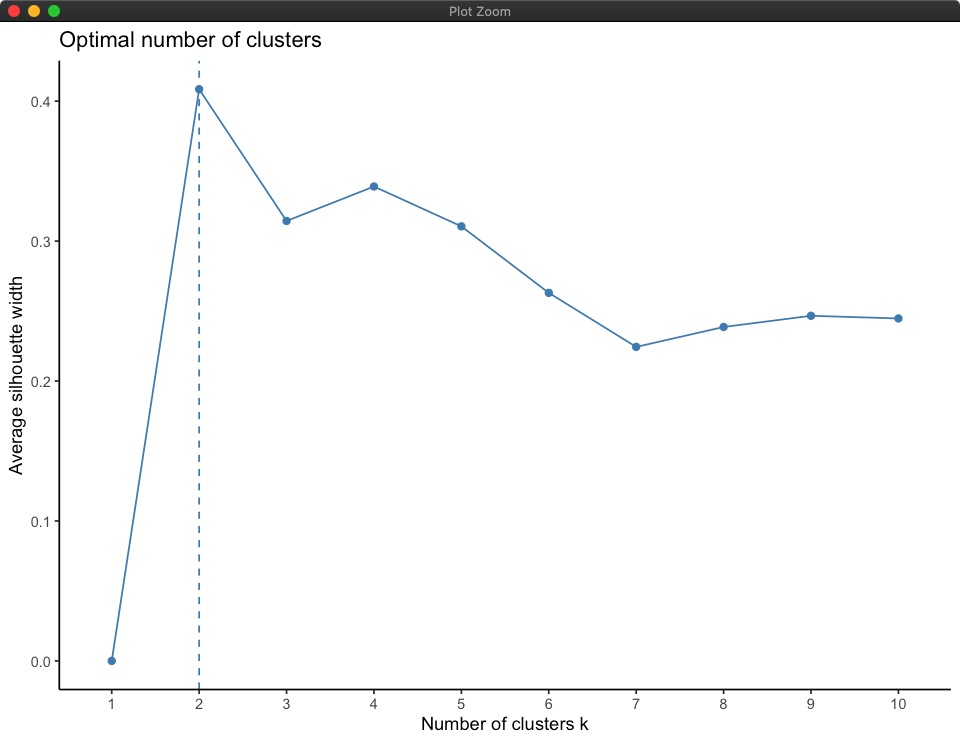
最佳聚类数为2:
pam_res <- pam(df_scaled,2)
names(pam_res)
# [1] "medoids" "id.med" "clustering" "objective" "isolation" "clusinfo"
# [7] "silinfo" "diss" "call" "data"
继续使用fviz_cluster进行PCA降维后可视化聚类的效果:
fviz_cluster(pam_res, data = df_scaled)
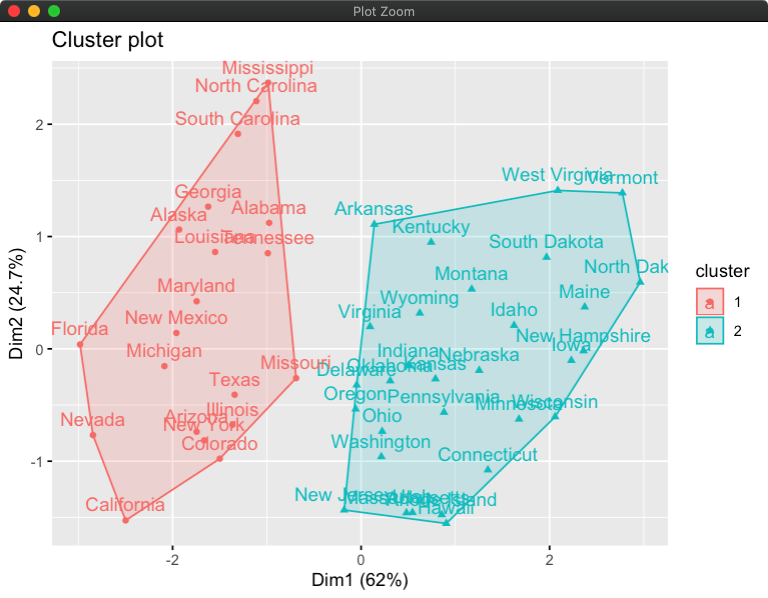
CLARA聚类
CLARA (Clustering Large Applications)是k-medoids聚类的延伸,用来处理比较大的数据集
算法
- 随机将数据集分成几个固定样本数量的亚数据集
- 应用PAM算法找出每个亚数据集的中心点,分别将每个亚数据集的中心点应用到整个数据集
- 计算所有数据点到最近中心点的距离和,保留最小距离和的亚数据集的中心点
- 重复1,2步如果计算的距离和小于上次最小的距离和则用新的中心点代替原来的中心点直至中心点不再变化
R
##generate data
set.seed(2020721)
df <- rbind(cbind(rnorm(200,0,8), rnorm(200,0,8)),
cbind(rnorm(300,50,8), rnorm(300,50,8)))
colnames(df) <- c("x","y")
rownames(df) <- paste("S",1:nrow(df),sep = "")
cluster::clara(x, k, metric = "euclidean", stand = FALSE, samples = 5, pamLike = FALSE)
- x: 数值矩阵或者数据框,行是观测,列是变量
- k: 聚类数
- metric : 距离计算方法可以选择euclidean或者manhattan
- stand:是否要标准化
- samples:从数据集中抽取的样本数量
- pamLike:是否和
pam()函数使用相同的算法
首先使用silhouette方法来估计最佳聚类数:
fviz_nbclust(df, clara, method = "silhouette")+
theme_classic()

最佳聚类数为2:
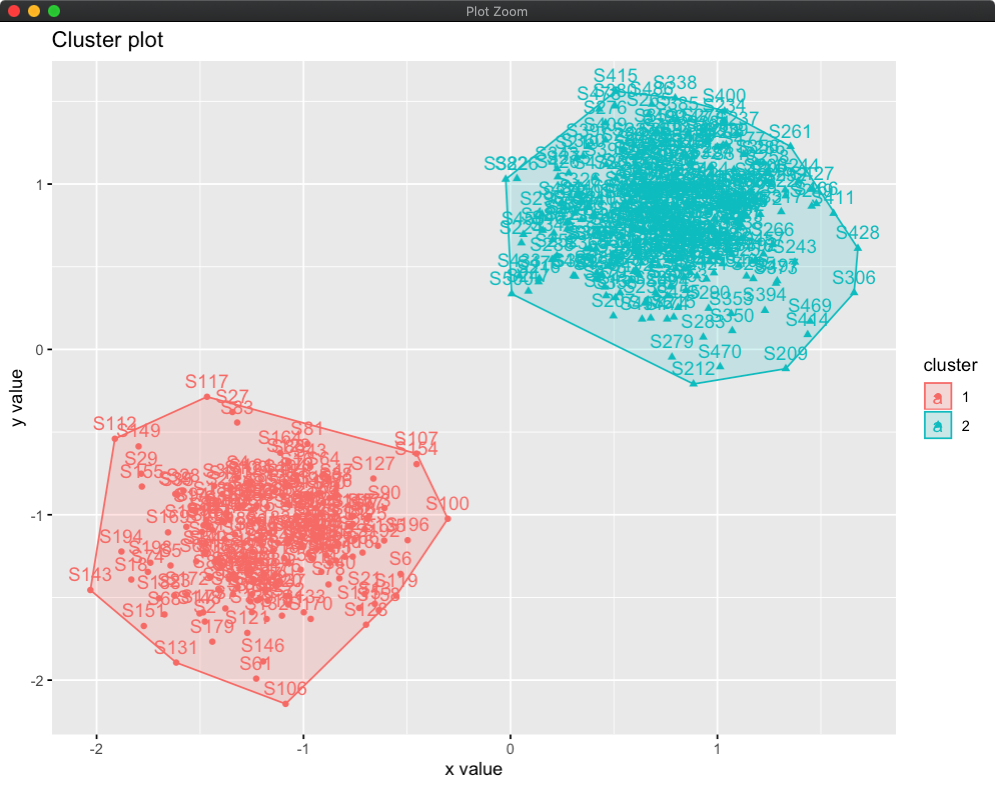
clara_res <- clara(df,2,samples = 50,pamLike = T)
print(clara_res)
names(clara_res)
# [1] "sample" "medoids" "i.med" "clustering" "objective" "clusinfo"
# [7] "diss" "call" "silinfo" "data"
fviz_cluster(clara_res,data = df)
层次聚类(Hierarchical clustering)
层次聚类和划分聚类一个显著不同就是层次聚类不需要预先规定聚类数目
- 凝聚方法(agglomerative hierarchical clustering):自底向上,每个观察值最初都被视为一类(叶),然后将最相似的类连续合并,直到只有一个大类(根)为止
- 分裂方法(divisive hierarchical clustering):自上向下,是凝聚聚类的逆过程,从根开始,所有观测值都包含在一个类中然后将最不均一的聚类相继划分直到所有观测值都在它们自己的类中(叶)
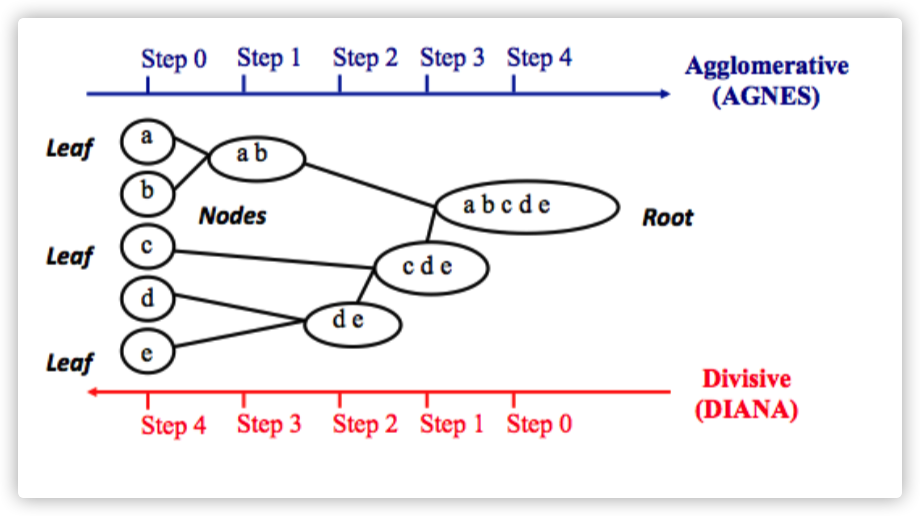
凝聚聚类
- 准备数据,计算距离矩阵
- 使用连接函数(linkage function)基于距离信息将对象连接成层次聚类树
- 决定如何切割聚类树
连接函数获取由函数dist()返回的距离信息,并根据对象的相似性将对象对分组;重复此过程,直到原始数据集中的所有对象在层次树中链接在一起为止
res_hc <- stats::hclust(d = dist.eucl, method = "ward.D2")
- d: 距离矩阵(不相似性矩阵)
- method: 连接函数,可以是“ward.D”, “ward.D2”, “single”,“complete”, “average”, “mcquitty”, “median” “centroid”
主要使用的连接函数(也就是类间距离)有:
- 最长距离法(complete-linkage):两个类的距离定义为两个类的元素的所有成对距离的最大值
- 最短距离法(single-linkage): 两个类的距离定义为两个类的元素的所有成对距离的最小值
- 类平均法(mean or average linkage,UPGMA): 两个类的距离定义为两个类的元素的所有成对距离的平均值
- 中心法(centroid linkage,UPGMC): 两个聚类之间的距离定义为两个类的质心(centroid,该类所有点的均值)的距离
- Ward法: 最小化总的within-cluster variation
plot(res_hc)
fviz_dend(res_hc, cex = 0.5)
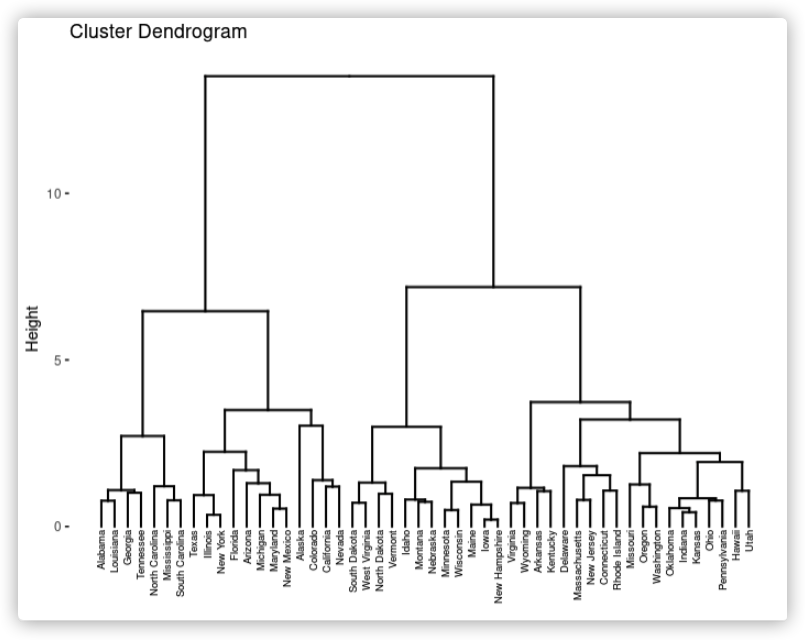
连接两个对象的竖线的高度衡量了这两个对象的距离,越长距离越大,这个高度也叫这两个对象的共同距离cophenetic distance
两个点的共同距离是这两个点第一次被聚在一起时的节点的高度,截取一小部分说明:
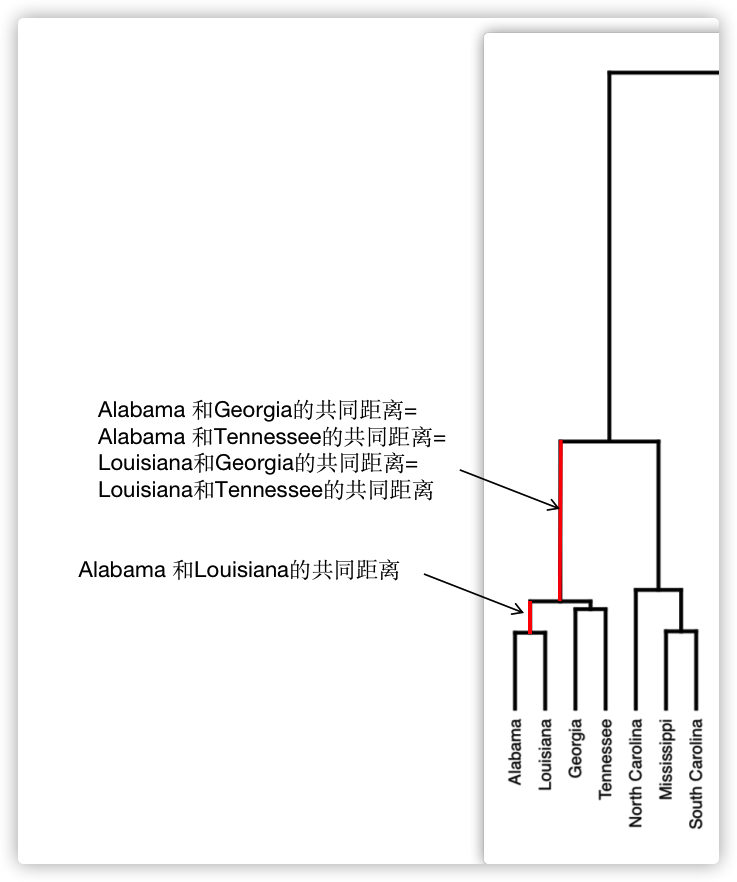
我们可以看聚类树的共同距离和原始的距离矩阵的相似性来衡量聚类的好坏:
res_coph <- cophenetic(res_hc)
cor(dist_eucl, res_coph)#[1] 0.6975266
res_hc2 <- hclust(dist_eucl, method = "average") ##类平均法
cor(dist_eucl, cophenetic(res_hc2))#[1] 0.7180382
可以使用cutree函数来分割树进行聚类结果的展示:
cluster <- cutree(res_hc, k = 4)
table(cluster)
# cluster
# 1 2 3 4
# 7 12 19 12
factoextra::fviz_dend(res_hc, k = 4,rect = TRUE)##可视化
fviz_cluster(list(data = df_scaled, cluster = cluster))##先PCA再展现聚类结果
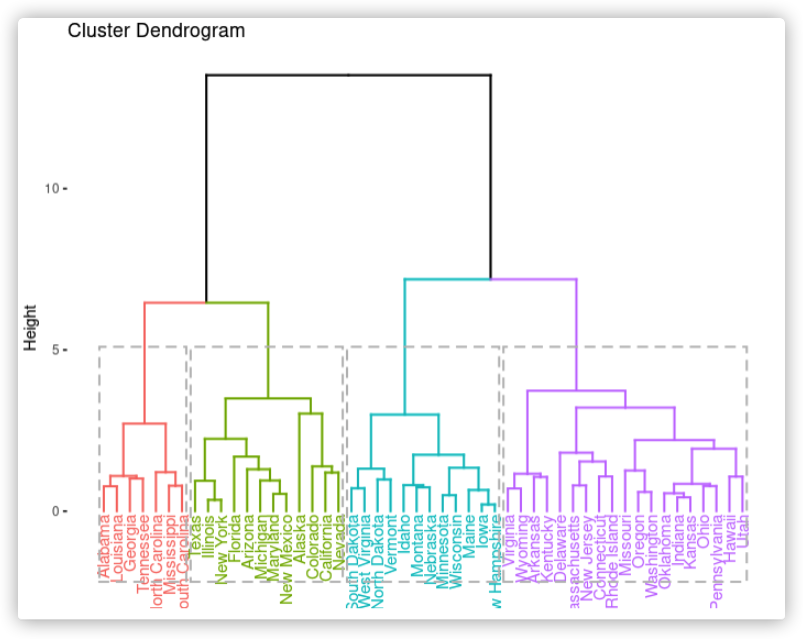
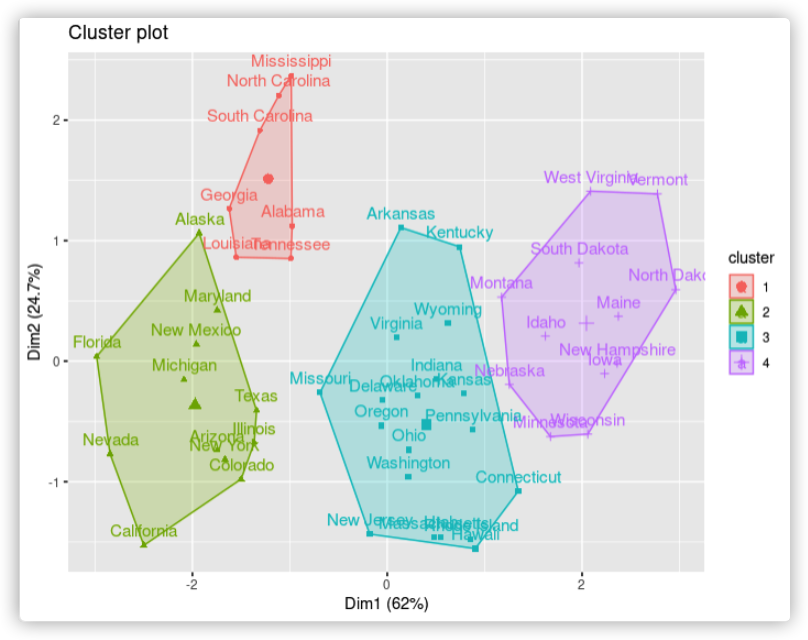
另外cluster包也可以很方便的进行凝聚或者分裂聚类:
library("cluster")
# Agglomerative
res.agnes <- agnes(x = USArrests, # data matrix
stand = TRUE, # Standardize the data
metric = "euclidean", # metric for distance matrix method = "ward" # Linkage method
)
# Divisive
res.diana <- diana(x = USArrests, # data matrix
stand = TRUE, # standardize the data
metric = "euclidean" # metric for distance matrix
)
比较树状图
使用dendextend包
首先创建两个不同的树状图:
dend1 <- stats::as.dendrogram(res_hc)
dend2 <- stats::as.dendrogram(res_hc2)
dend_list <- dendextend::dendlist(dend1, dend2)
dendextend::tanglegram(dend1, dend2)
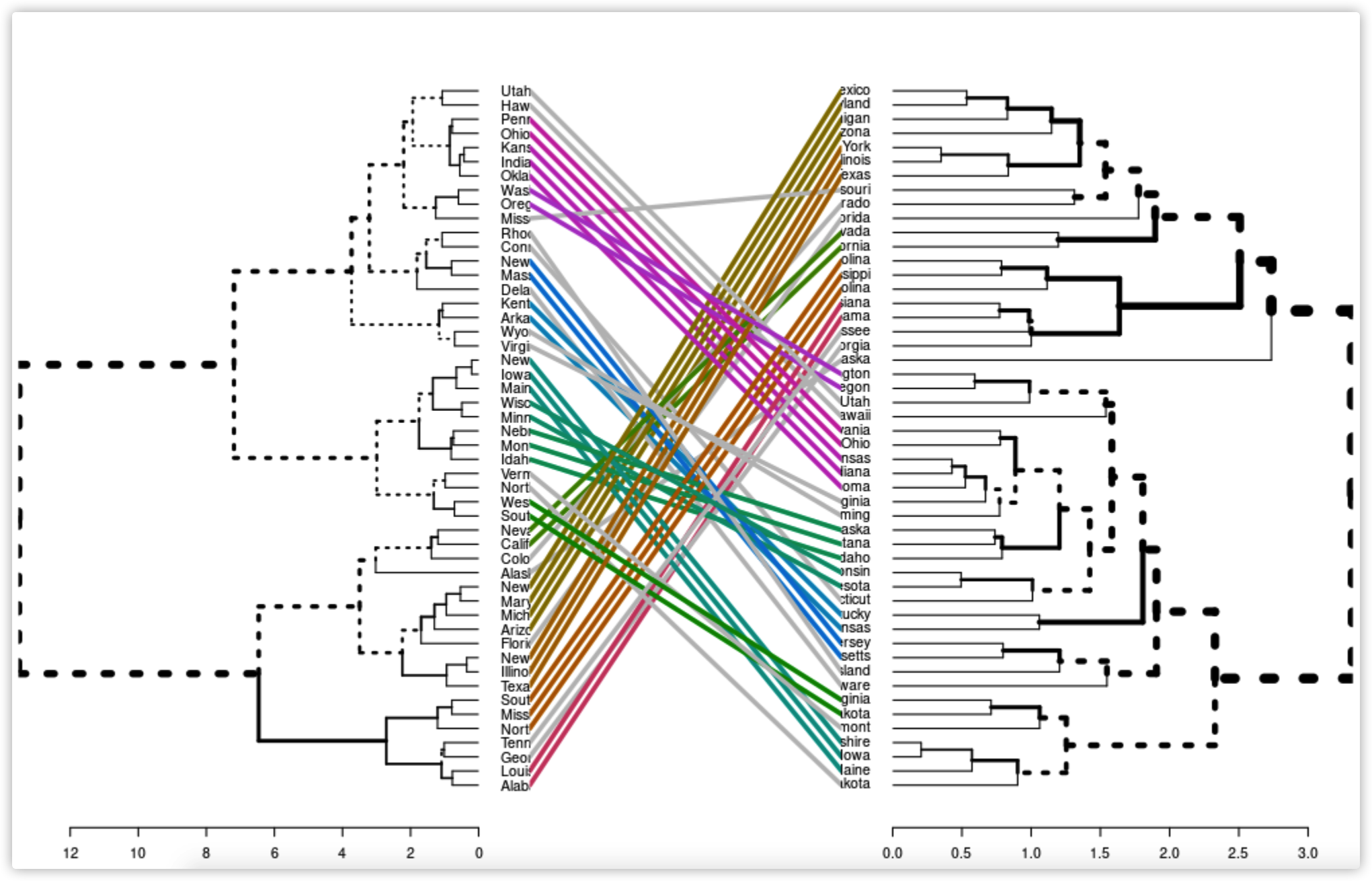
比对的质量可以使用entanglement()函数来计算,这个值是0到1之间的,越小说明比对越好
dendextend::entanglement(dend1, dend2)
#[1] 0.8342094
也可以使用cor.dendlist()函数来计算两个树的相关性,有两种方法cophenetic和baker
# Cophenetic correlation matrix
dendextend::cor.dendlist(dend_list, method = "cophenetic")
# [,1] [,2]
# [1,] 1.000000 0.843143
# [2,] 0.843143 1.000000
# Baker correlation matrix
dendextend::cor.dendlist(dend_list, method = "baker")
# [,1] [,2]
# [1,] 1.0000000 0.8400675
# [2,] 0.8400675 1.0000000
选择最佳聚类数
- 直接法:最优化一个准则,比如within cluster variation(肘方法,elbow method)或者平均轮廓(轮廓法,silhouette method)
- 统计检验的方法:比如gap 统计量检验法
- Elbow method(肘方法)
将总的WSS看做是聚类数的函数,当增加聚类数不会大幅度降低WSS时会出现一个拐点,选择该点作为最佳聚类数
- Average silhouette method(平均轮廓法)
该方法需要计算轮廓系数:
计算对象i到同类其他对象的平均距离$a_i$,$a_i$越小,说明样本i越应该被聚类到该类,将$a_i$称为样本i的簇内不相似度,类的所有对象的$a_i$均值称为该类的类不相似度;计算对象i到其他某类Cj 的所有对象的平均距离$b_{ij}$,称为样本i与簇Cj 的不相似度,对象i的类间不相似度:$bi =min({b_{i1}, b_{i2}, …, b_{ik}})$;根据类内不相似度和类间不相似度可以计算对象i的轮廓系数:

所有样本的$s_i$的均值称为聚类结果的轮廓系数,是该聚类是否合理、有效的度量
和肘方法相似,计算不同聚类数目的轮廓系数,轮廓系数最大的聚类数为最佳聚类数
- Gap statistic method
- 对不同的聚类数算出相应的within cluster variation:$W_k$
- 产生B个随机均匀分布的参考数据集,然后对这个数据集进行聚类,计算不同聚类数的within cluster variation :$W_{kb}$
- 计算估计的gap统计量 $Gap(k)=\frac{1}{B}\sum^B_{b=1}log(W_{kb})-log(W_k)$
- 选择满足$Gap(k)\geq Gap_{k+1}-s_{k+1}(标准差)$ 的最小的k作为最优的聚类个数
一般选择B=500,结果就比较稳健
R
factoextra::fviz_nbclust(x, FUNcluster, method = c("silhouette", "wss", "gap_stat"))
- x: 数值矩阵或者数据框
- FUNcluster: 聚类方法包括kmeans, pam, clara 和 hcut
- method: 决定最佳聚类数的方法
# Elbow method
p1 <- factoextra::fviz_nbclust(df_scaled, kmeans, method = "wss") +
geom_vline(xintercept = 4, linetype = 2)+
labs(subtitle = "Elbow method")
# Silhouette method
p2 <- factoextra::fviz_nbclust(df_scaled, kmeans, method = "silhouette")+
labs(subtitle = "Silhouette method")
# Gap statistic
# nboot = 50 to keep the function speedy.
# recommended value: nboot= 500 for your analysis.
# Use verbose = FALSE to hide computing progression.
set.seed(123)
p3 <- factoextra::fviz_nbclust(df_scaled, kmeans, nstart = 25, method = "gap_stat", nboot = 50)+
labs(subtitle = "Gap statistic method")
cowplot::plot_grid(p1,p2,p3)
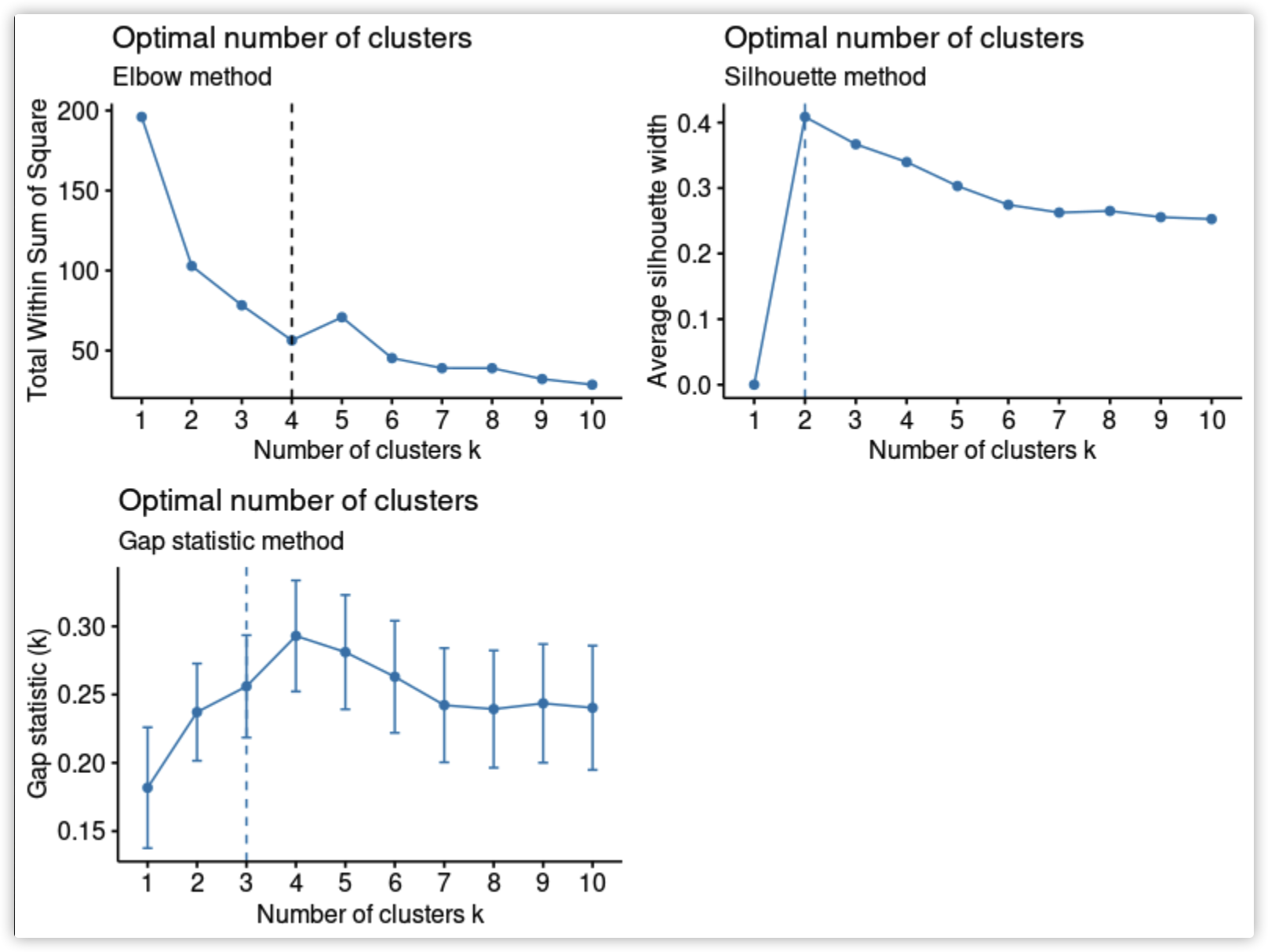
NbClust包的NbClust()函数可以提供30种指标来计算最佳聚类数
NbClust(data = NULL, diss = NULL,
distance = "euclidean", min.nc = 2, max.nc = 15, method = NULL)
- data : 矩阵
- diss:不相似矩阵,如果提供diss,后面的distance应该为NULL
- distance: 计算距离矩阵的方法包括euclidean manhattan和NULL
- min.nc, max.nc:最小最大的聚类数
- method: 聚类方法”ward.D”, “ward.D2”, “single”, “complete”, “average”, “mcquitty”, “median”, “centroid”, “kmeans”
nb <- NbClust::NbClust(df_scaled, distance = "euclidean", min.nc = 2,
max.nc = 10, method = "kmeans")
factoextra::fviz_nbclust(nb)
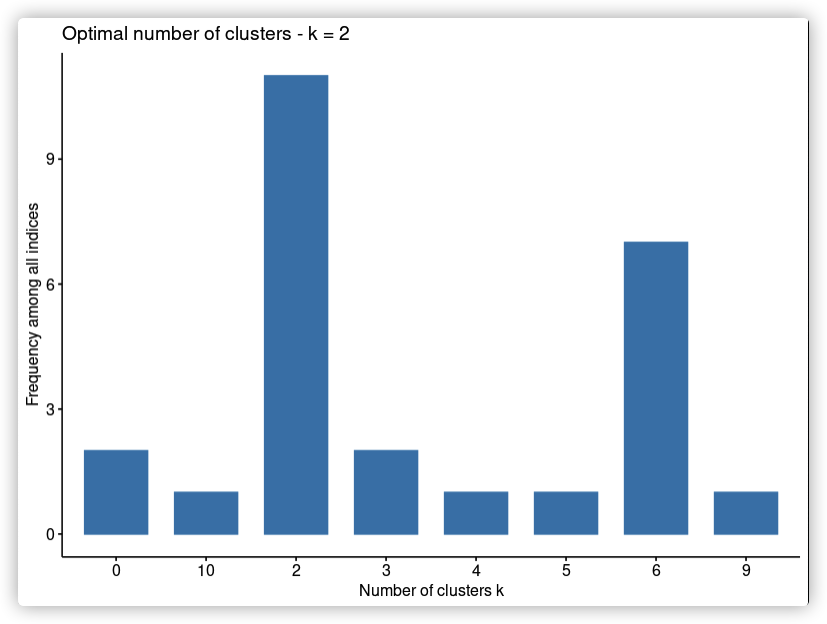
还有一个增强版的hclust:fastcluster::hclust:更快,能处理更大的数据

参考:
https://cran.r-project.org/web/packages/flashClust/index.html
https://www.biostars.org/p/85150/
https://www.cnblogs.com/lexus/archive/2012/12/13/2815769.html
Kassambara A. Practical guide to cluster analysis in R: Unsupervised machine learning[M]. Sthda, 2017.