分析技术研习室
课题组每周研讨会
主要内容来自深度学习入门:

感知机
感知机也可以称为人工神经元,是神经网络的基础
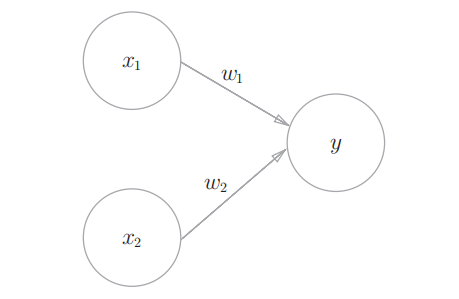
感知机接受多个信号(x1,x2),输出一个信号(y), w1/w2是权重,圆圈就代表神经元
输入信号被传递到神经元的时候会被乘上权重(w1x1、w2x2),神经元会计算输入的信号总和,只有这个总和超过某个阈值才会输出1,这个状态就叫做神经元的激活,这个过程用函数表示如下( $\theta$表示阈值):
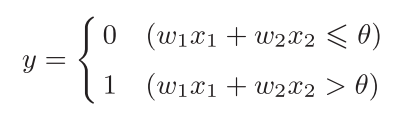
也可以对上式进行形式上的转化(将$\theta$移到左边):
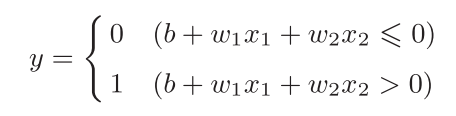
这里面b叫做偏置
可以看出w1和w2是控制输入信号的重要性的参数,而偏置b是调整神经元被激活的容易程度的参数
我们再进一步简化上面函数的形式,引入一个新的函数$h(x)$,将上面的函数改写:
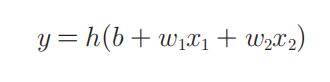
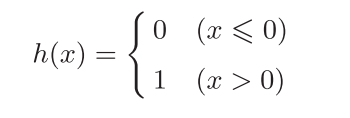
函数$h(x)$对输入信号的总和进行转化,转化后的值就是输出y
这个函数$h(x)$就是激活函数
我们可以将上面的感知机进行细化,展示出激活函数的运算过程:
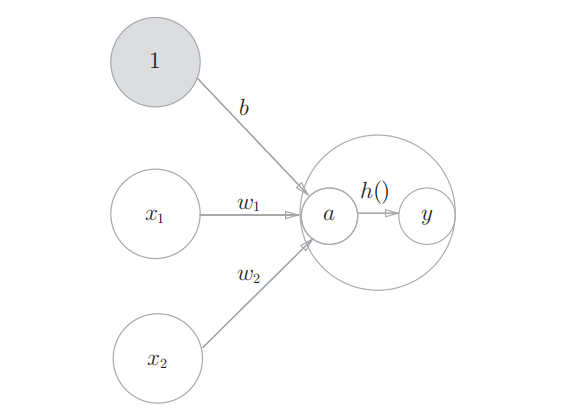
$a=w_1x_1+w_2x_2+b$, $y=h(a)$
a计算计算加权输入信号和偏置的总和,用h(x)函数将a转换为输出y
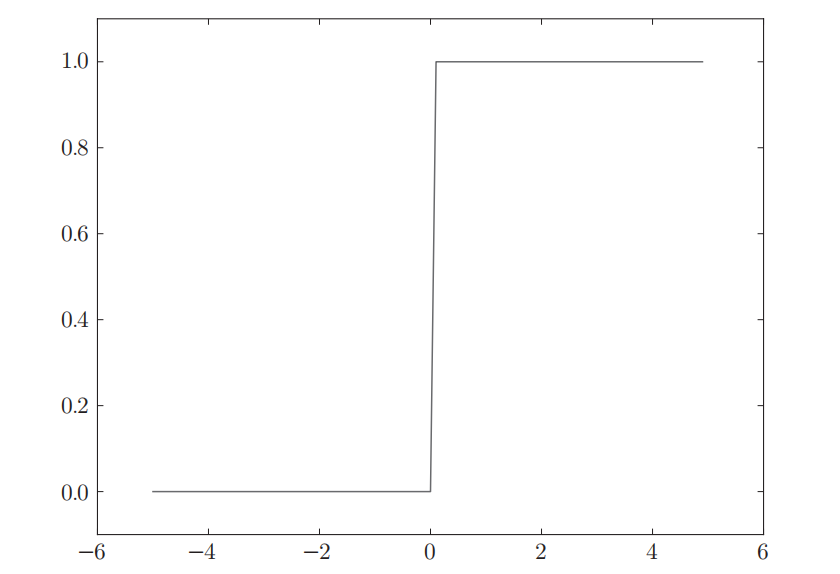
这样的激活函数称为阶跃函数,超过某个阈值就会改变函数的输出,函数的图像呈阶梯状:
神经网络
神经网络可以看作是多层感知机,并且使用的激活函数不再是阶跃函数了
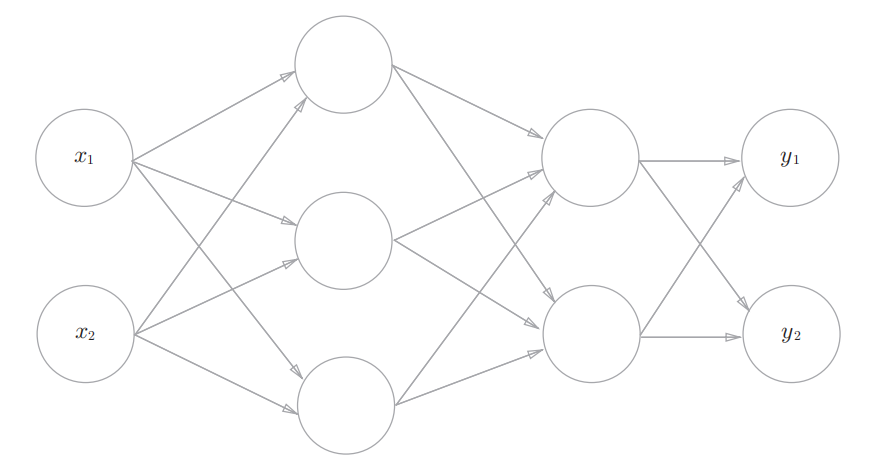
上图展示的是一个简单的3层(从0开始计算)神经网络
先来看一下常用的激活函数:
sigmoid函数
sigmoid函数的表示为:
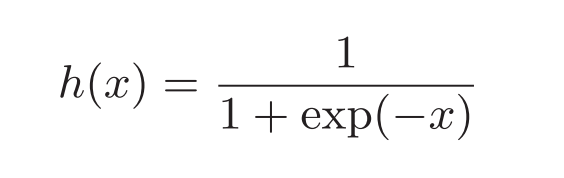
可以通过python简单的实现:
import numpy as np
import matplotlib.pylab as plt
###sigmoid function
def sigmoid(x):
return 1 / (1 + np.exp(-x))
X = np.arange(-5.0, 5.0, 0.1)
Y = sigmoid(X)
plt.plot(X, Y)
plt.ylim(-0.1, 1.1)
plt.show()
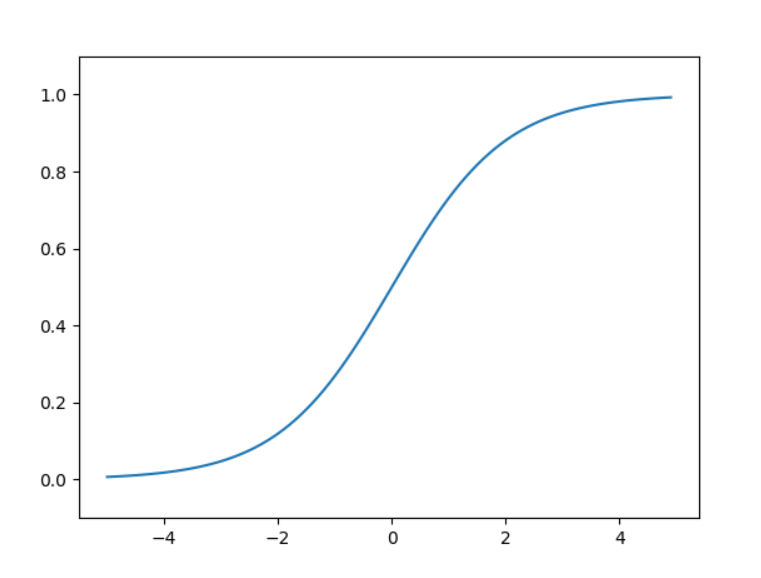
sigmoid函数和阶跃函数的主要区别在于其是平滑的曲线,连续可导
ReLU函数
ReLU全称为Rectified Linear Unit,线性整流函数
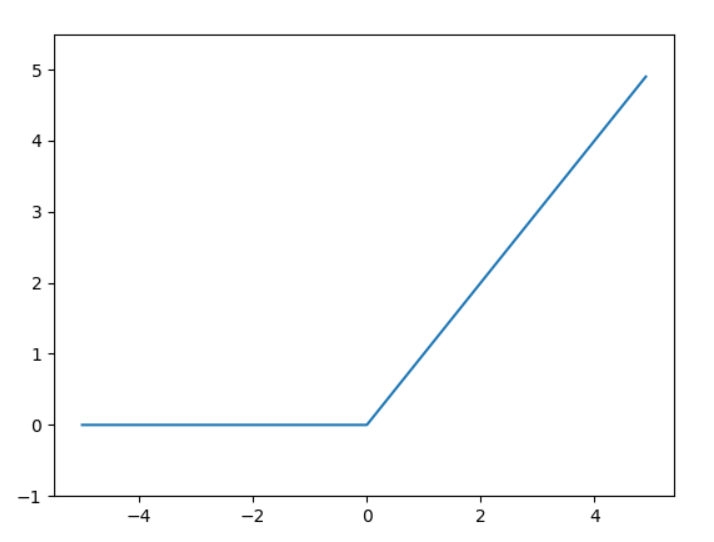
ReLU函数在输入大于0时,直接输出该值;在输入小于等于0时,输出0:
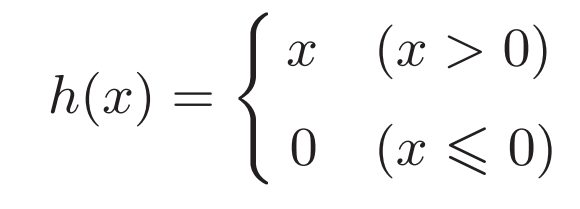
##relu
def relu(x):
return np.maximum(0, x)
x = np.arange(-5.0, 5.0, 0.1)
y = relu(x)
plt.plot(x, y)
plt.ylim(-1.0, 5.5)
plt.show()
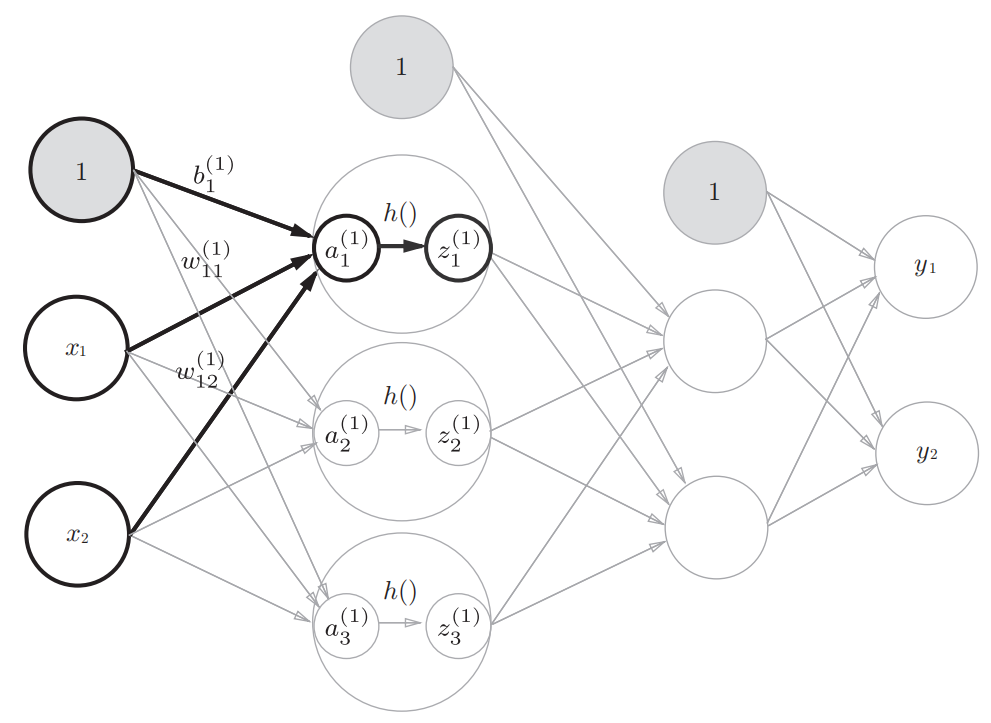
3层神经网络的实现
各层间信号的传递可以用下图来表示:
#####three layer network
def init_network():
network = {}
network['W1'] = np.array([[0.1, 0.3, 0.5], [0.2, 0.4, 0.6]])
network['b1'] = np.array([0.1, 0.2, 0.3])
network['W2'] = np.array([[0.1, 0.4], [0.2, 0.5], [0.3, 0.6]])
network['b2'] = np.array([0.1, 0.2])
network['W3'] = np.array([[0.1, 0.3], [0.2, 0.4]])
network['b3'] = np.array([0.1, 0.2])
return network
def forward(network, x):
W1, W2, W3 = network['W1'], network['W2'], network['W3']
b1, b2, b3 = network['b1'], network['b2'], network['b3']
a1 = np.dot(x, W1) + b1
z1 = sigmoid(a1)
a2 = np.dot(z1, W2) + b2
z2 = sigmoid(a2)
a3 = np.dot(z2, W3) + b3
y = identity_function(a3)
return y
network = init_network()
x = np.array([1.0, 0.5])##初始输入
y = forward(network, x)
print(y)
这里面需要注意的点是输出层的激活函数使用的是恒等函数,一般地,回归问题可以使用恒等函数,二元分类问题可以使用 sigmoid函数,多元分类问题可以使用 softmax函数
softmax函数可以表示为:

但是这个函数在进行计算的时候,指数运算可能会产生非常大的数(可能会出现Inf),需要对其进行变换:

可以将$C’$替换为输入信号的最大值的负值来减小运算:
def softmax(a):
c = np.max(a)
exp_a = np.exp(a - c) # 溢出对策
sum_exp_a = np.sum(exp_a)
y = exp_a / sum_exp_a
return y
a = np.array([0.3, 2.9, 4.0])
y = softmax(a)
print(y)#[0.01821127 0.24519181 0.73659691]
np.sum(y)#1.0
softmax函数会将输入信号映射到0~1上,并且转化后的值总和为1,这就使我们可以把softmax函数的输出解释为
概率值;另外指数函数在求导时也比较方便(导数还是指数函数)
神经网络的学习
神经网络的学习过程就是通过某种指标来寻找最优权重参数,这个指标就称为损失函数,损失函数表示的是神经网络对当前训练数据在多大程度上不拟合,所以目标就是使损失函数尽可能小
损失函数一般使用均方误差和交叉熵误差
均方误差如下所示:
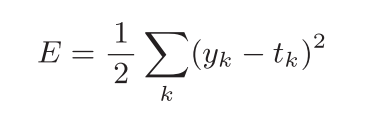
y表示神经网络得输出,t表示训练数据,k表示维度
分类问题和回归问题都可以使用均方误差
###mean_squared_error
def mean_squared_error(y, t):
return 0.5 * np.sum((y-t)**2)
t = [0, 0, 1, 0, 0, 0, 0, 0, 0, 0]
y = [0.1, 0.05, 0.6, 0.0, 0.05, 0.1, 0.0, 0.1, 0.0, 0.0]
mean_squared_error(np.array(y), np.array(t))
##0.09750000000000003
y = [0.1, 0.05, 0.1, 0.0, 0.05, 0.1, 0.0, 0.6, 0.0, 0.0]
mean_squared_error(np.array(y), np.array(t))
##0.5975
交叉熵误差一般作为分类问题的损失函数:
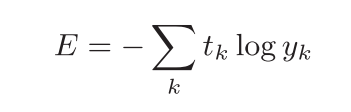
y表示神经网络的输出,t表示训练数据的标签,相应的类标签为1,其他为0,所以交叉熵误差只计算正确标签对应的神经网络的输出,当这个输出越接近于1,E值就越小(等于1时,E=0)
def cross_entropy_error(y, t):
delta = 1e-7
return -np.sum(t * np.log(y + delta))
t = [0, 0, 1, 0, 0, 0, 0, 0, 0, 0]
y = [0.1, 0.05, 0.6, 0.0, 0.05, 0.1, 0.0, 0.1, 0.0, 0.0]
cross_entropy_error(np.array(y), np.array(t))
##0.510825457099338
y = [0.1, 0.05, 0.1, 0.0, 0.05, 0.1, 0.0, 0.6, 0.0, 0.0]
cross_entropy_error(np.array(y), np.array(t))
##2.302584092994546
神经网络学习的任务就是找到损失函数取最小值(或尽可能小)时的参数(权重和偏置),这个过程可以通过梯度法来实现
梯度
在介绍梯度之前需要知道导数的概念
导数表示的是某个瞬间的变化量,即x的微小变化将导致函数f(x)的值在多大程度上发生变化:

在实现求导的时候,可以人为导入一个微小的h,并且使用中心差分的形式($f(x+h)-f(x-h)$,以x为中心可以减少误差)
def numerical_diff(f, x):
h = 1e-4
return (f(x+h) - f(x-h)) / (2*h)
这种通过微小的差分来求导数的过程称为数值微分,和利用数学推导求导数的解析性求导区分
当我们需要对有多个变量的函数中每个变量进行求导,这个时候的导数就叫做偏导数,求偏导数就是将某个变量定为目标变量,其余变量固定为常数,然后对目标变量求导的过程
比如有一个二变量的函数:$f(x_0,x_1)=x_0^2+x_1^2$ ,求$x_0=3,x_1=4$的时候,关于各个变量的偏导数
##定义函数
def function_2(x):
return x[0]**2 + x[1]**2
求偏导就是将无关的变量设为常量:
##x0
def function_tmp1(x0):
return x0*x0 + 4.0**2.0
numerical_diff(function_tmp1, 3.0)#6.00000000000378
##x1
def function_tmp2(x1):
return 3.0**2.0 + x1*x1
numerical_diff(function_tmp2, 4.0)#7.999999999999119
由全部变量的偏导数汇总而成的向量称为梯度(gradient)比如对于上面的二变量函数,梯度就是$(\frac{\partial f}{\partial x_0},\frac{\partial f}{\partial x_1})$ 构成的向量:
def numerical_gradient(f, x):
h = 1e-4
grad = np.zeros_like(x) # 生成和x形状相同的数组
for idx in range(x.size):
tmp_val = x[idx]
# f(x+h)的计算
x[idx] = tmp_val + h
fxh1 = f(x)
# f(x-h)的计算
x[idx] = tmp_val - h
fxh2 = f(x)
grad[idx] = (fxh1 - fxh2) / (2*h)
x[idx] = tmp_val # 还原值
return grad
numerical_gradient(function_2, np.array([3.0, 4.0]))
#array([6., 8.])
计算这个函数各点的梯度:
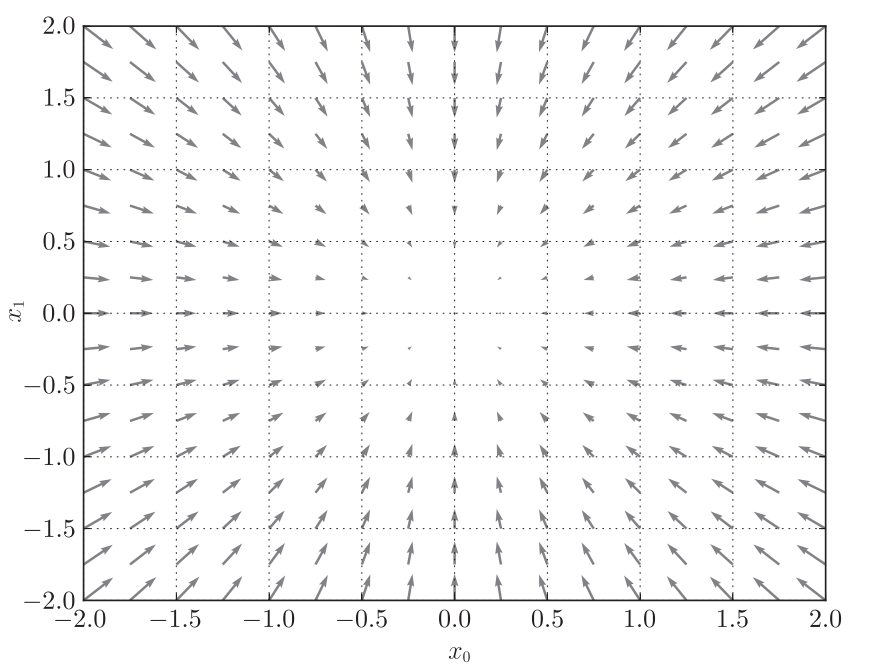
这个箭头就代表了梯度,可以看到梯度的方向指向这个函数的最小值(0,0); 虽然在其他情况下梯度的方向并不总是指向最小值,但沿着它的方向能够最大限度地减小函数的值;因此通过不断地沿梯度方向前进,逐渐减小函数值的过程就是梯度法(gradient method)(一般指的的梯度下降)
用数学式表示梯度法:
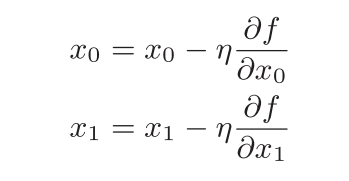
其中η表示更新量,表示每次沿着梯度的方向下降的程度,在神经网络中称为学习率(learning rate)
##gradient_descent
##f 进行最优化的函数
##init_x 初始值
##lr 学习率
##step_num 迭代次数
def gradient_descent(f, init_x, lr=0.01, step_num=100):
x = init_x
for i in range(step_num):
grad = numerical_gradient(f, x)
x -= lr * grad
return x
init_x = np.array([-3.0, 4.0])
gradient_descent(function_2, init_x=init_x, lr=0.1, step_num=100)
#array([-6.11110793e-10, 8.14814391e-10])
像学习率这样的参数称为超参数 , 神经网络的权重参数是通过学习得到的,而超参数是人为设定的,所以需要尝试
学习算法的实现
神经网络的学习步骤可以分成以下几步:
- mini-batch: 从训练数据中随机选出一部分数据,这部分数据称为mini batch。我们的目标是减小mini batch的损失函数的值
- 计算梯度:为了减小mini batch的损失函数的值,需要求出各个权重参数的梯度;梯度表示损失函数的值减小最多的方向
- 更新参数:将权重参数沿梯度方向进行微小更新
- 迭代:重复前3个步骤
由于选择mini batch是随机的,因此这种方法叫做随机梯度下降法(stochastic gradient descent,SGD)
下面是两层神经网络的实现:
###TwoLayerNet
class TwoLayerNet:
def __init__(self, input_size, hidden_size, output_size, weight_init_std=0.01):
# 初始化权重
self.params = {}
self.params['W1'] = weight_init_std * np.random.randn(input_size, hidden_size)
self.params['b1'] = np.zeros(hidden_size)
self.params['W2'] = weight_init_std * np.random.randn(hidden_size, output_size)
self.params['b2'] = np.zeros(output_size)
def predict(self, x):
W1, W2 = self.params['W1'], self.params['W2']
b1, b2 = self.params['b1'], self.params['b2']
a1 = np.dot(x, W1) + b1
z1 = sigmoid(a1)
a2 = np.dot(z1, W2) + b2
y = softmax(a2)
return y
# x:输入数据, t:监督数据
def loss(self, x, t):
y = self.predict(x)
return cross_entropy_error(y, t)
def accuracy(self, x, t):
y = self.predict(x)
y = np.argmax(y, axis=1)
t = np.argmax(t, axis=1)
accuracy = np.sum(y == t) / float(x.shape[0])
return accuracy
# x:输入数据, t:监督数据
def numerical_gradient(self, x, t):
loss_W = lambda W: self.loss(x, t)
grads = {}
grads['W1'] = numerical_gradient(loss_W, self.params['W1'])
grads['b1'] = numerical_gradient(loss_W, self.params['b1'])
grads['W2'] = numerical_gradient(loss_W, self.params['W2'])
grads['b2'] = numerical_gradient(loss_W, self.params['b2'])
return grads
我们接下来在MNIST数据集上(MNIST的图像数据是28像素 × 28像素的灰度图像,各个像素的取值在0到255之间。每个图像数据都相应地标有相应的标签)利用这个两层神经网络实现手写体的识别:
###MNIST
# 读入数据
from dataset.mnist import load_mnist
(x_train, t_train), (x_test, t_test) = load_mnist(normalize=True, one_hot_label=True)
print(x_train.shape)
print(t_train.shape)
print(x_test.shape)
print(t_test.shape)
network = TwoLayerNet(input_size=784, hidden_size=50, output_size=10)
iters_num = 10000 # 适当设定循环的次数
train_size = x_train.shape[0]
batch_size = 100
learning_rate = 0.1
train_loss_list = []
train_acc_list = []
test_acc_list = []
##平均每个epoch的重复次数
iter_per_epoch = max(train_size / batch_size, 1)
for i in range(iters_num):
batch_mask = np.random.choice(train_size, batch_size)
x_batch = x_train[batch_mask]
t_batch = t_train[batch_mask]
# 计算梯度
grad = network.numerical_gradient(x_batch, t_batch)
# 更新参数
for key in ('W1', 'b1', 'W2', 'b2'):
network.params[key] -= learning_rate * grad[key]
##记录学习过程
loss = network.loss(x_batch, t_batch)
train_loss_list.append(loss)
#计算每个epoch的识别精度
if i % iter_per_epoch == 0:
train_acc = network.accuracy(x_train, t_train)
test_acc = network.accuracy(x_test, t_test)
train_acc_list.append(train_acc)
test_acc_list.append(test_acc)
print("train acc, test acc | " + str(train_acc) + ", " + str(test_acc))
# 绘制图形
markers = {'train': 'o', 'test': 's'}
x = np.arange(len(train_acc_list))
plt.plot(x, train_acc_list, label='train acc')
plt.plot(x, test_acc_list, label='test acc', linestyle='--')
plt.xlabel("epochs")
plt.ylabel("accuracy")
plt.ylim(0, 1.0)
plt.legend(loc='lower right')
plt.show()
先将所有训练数据随机打乱,然后按指定的批次大小,按序生成mini batch,给每个batch编号,按顺序遍历所有的batch,遍历一次所有的batch称为一个epoch(但是上面的实现是随机选取的)
误差反向传播算法
上面我们通过数值微分来计算权重参数的梯度,但是计算非常费时间,而误差反向传播算法就是一个可以高效计算权重参数的方法,这里通过计算图的方式来理解误差方向传播计算梯度的方法
先来介绍计算图:
问题是:超市买了2个100日元一个的苹果,消费税是10%,请计算支付金额
可以通过计算图来计算这个过程:
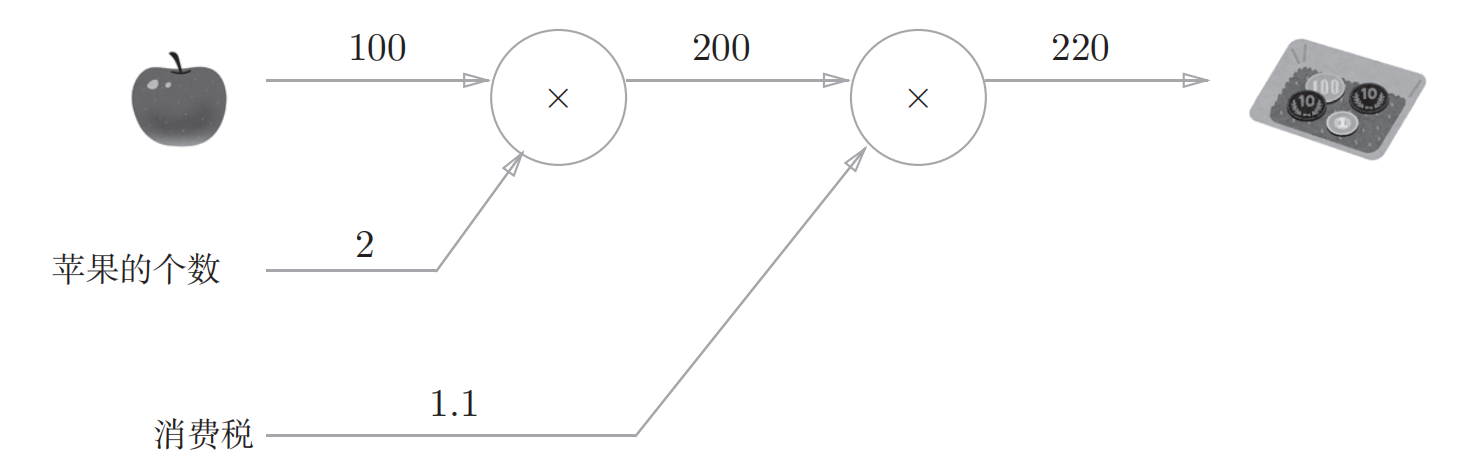
箭头上面标上结果,在节点内部进行计算
这种从左到右的计算方向称为正向传播,如果我们现在要计算苹果价格的波动会在多大程度上影响最终的支付金额,也就是要计算最终的支付金额对苹果价格的导数,这个时候就可以从右到左进行计算导数,这个过程就叫反向传播
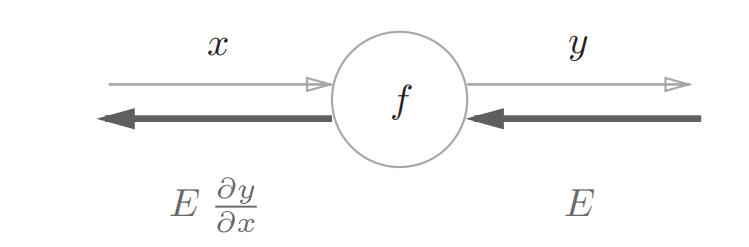
反向传播的计算顺序为:将传来的信号乘以局部导数再传递给下个节点
反向传播实现的关键是链式法则:
如果某个函数由复合函数表示,则该复合函数的导数可以用构成复合函数的各个函数的导数的乘积表示
举个例子:有一个函数:$z=(x+y)^2$是复合函数,可以拆成两个函数:
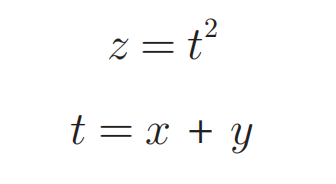
那么这个函数对x的偏导数就可以这样求:
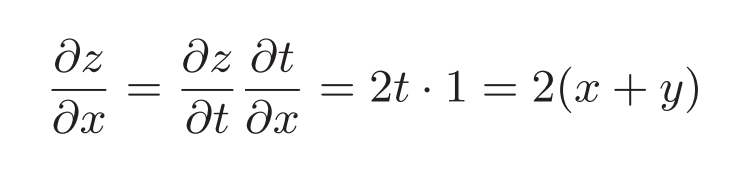
这个过程利用计算图求解如下:
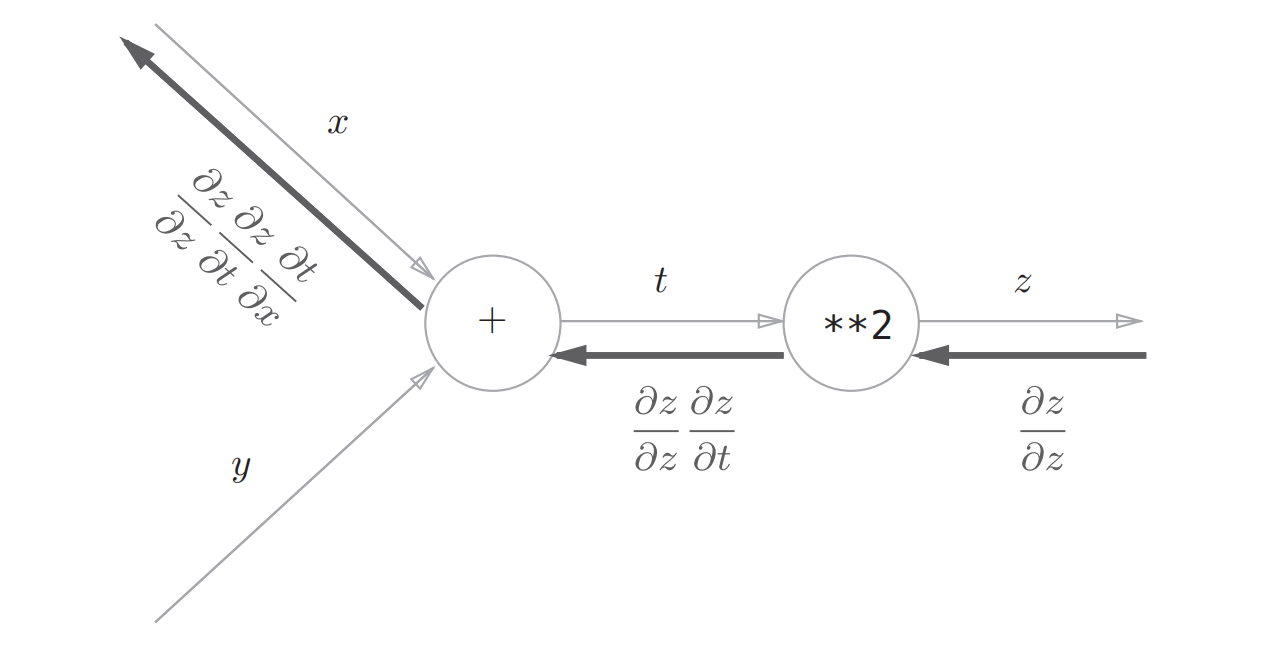
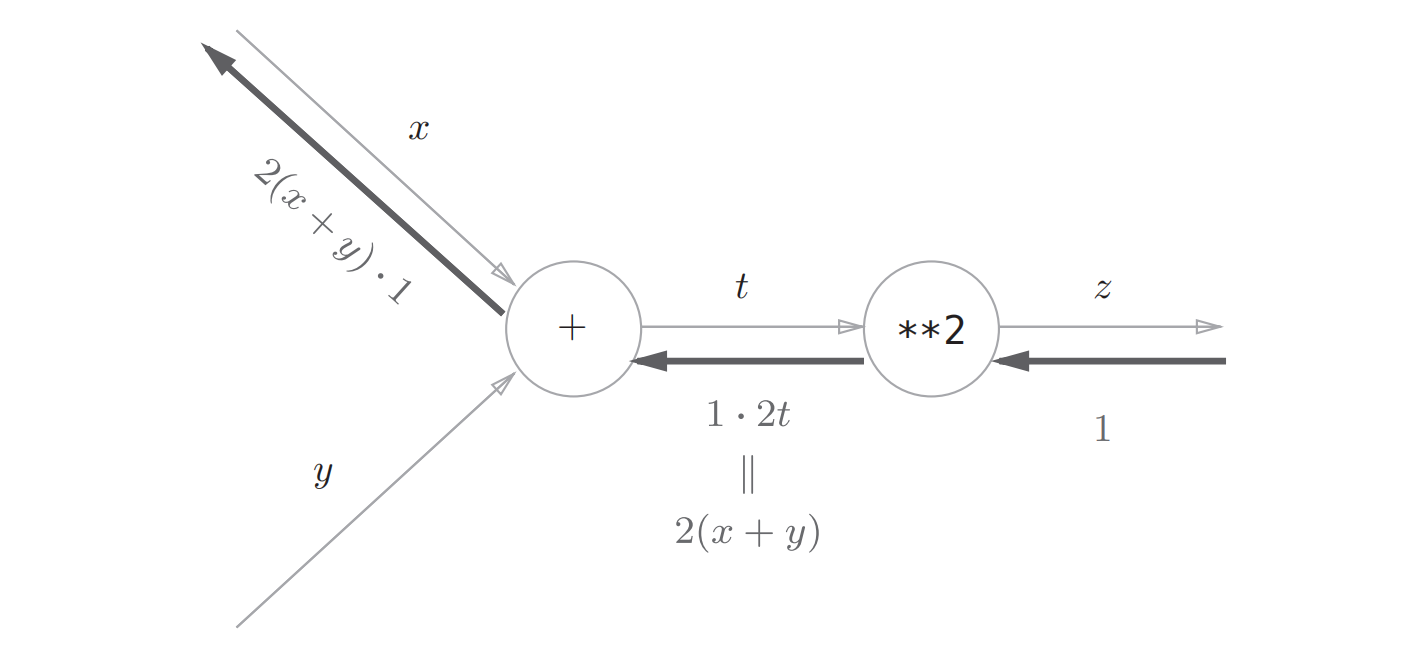
我们现在基于计算图来实现各个层的反向传播
首先是加法节点:
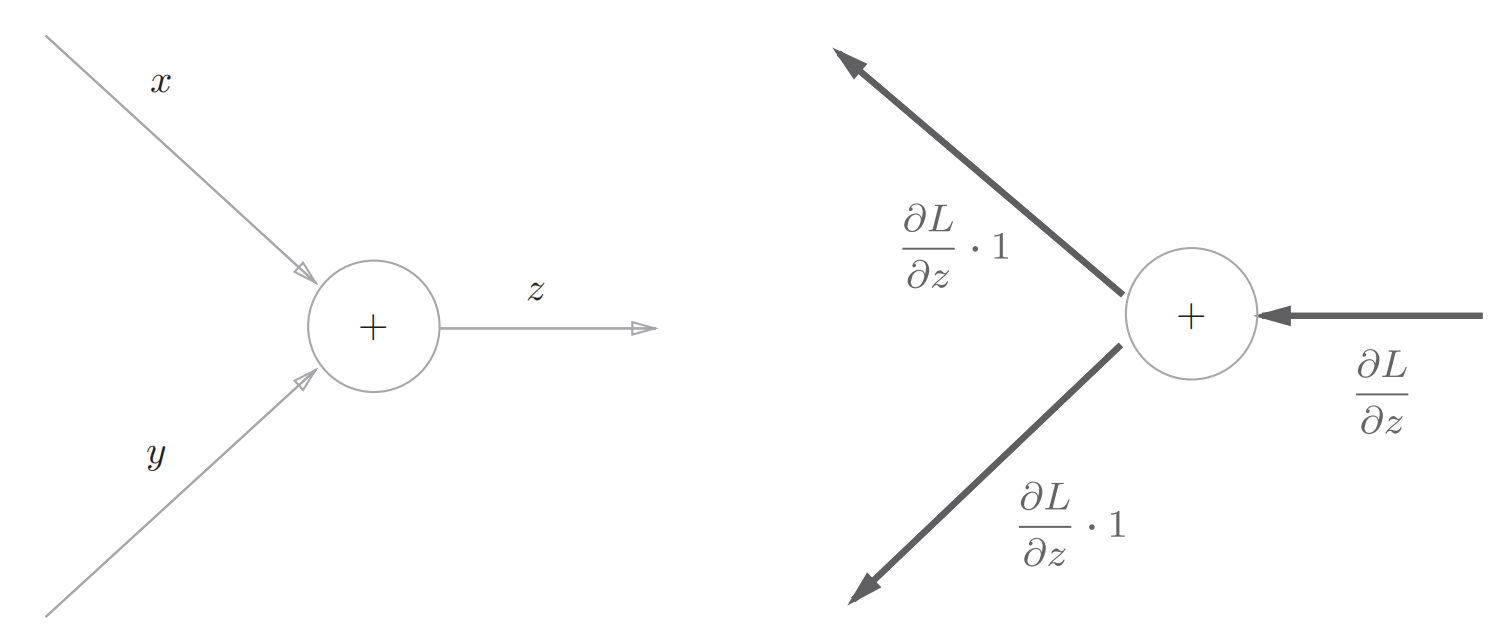
左边是正向传播,右边是反向传播
由于$\frac{\partial f}{\partial x}和\frac{\partial f}{\partial y}$都等于1,所以加法节点将上游的值原封不动地输出到下游
然后是乘法节点,考虑$z=xy$:
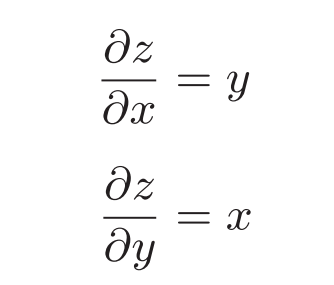
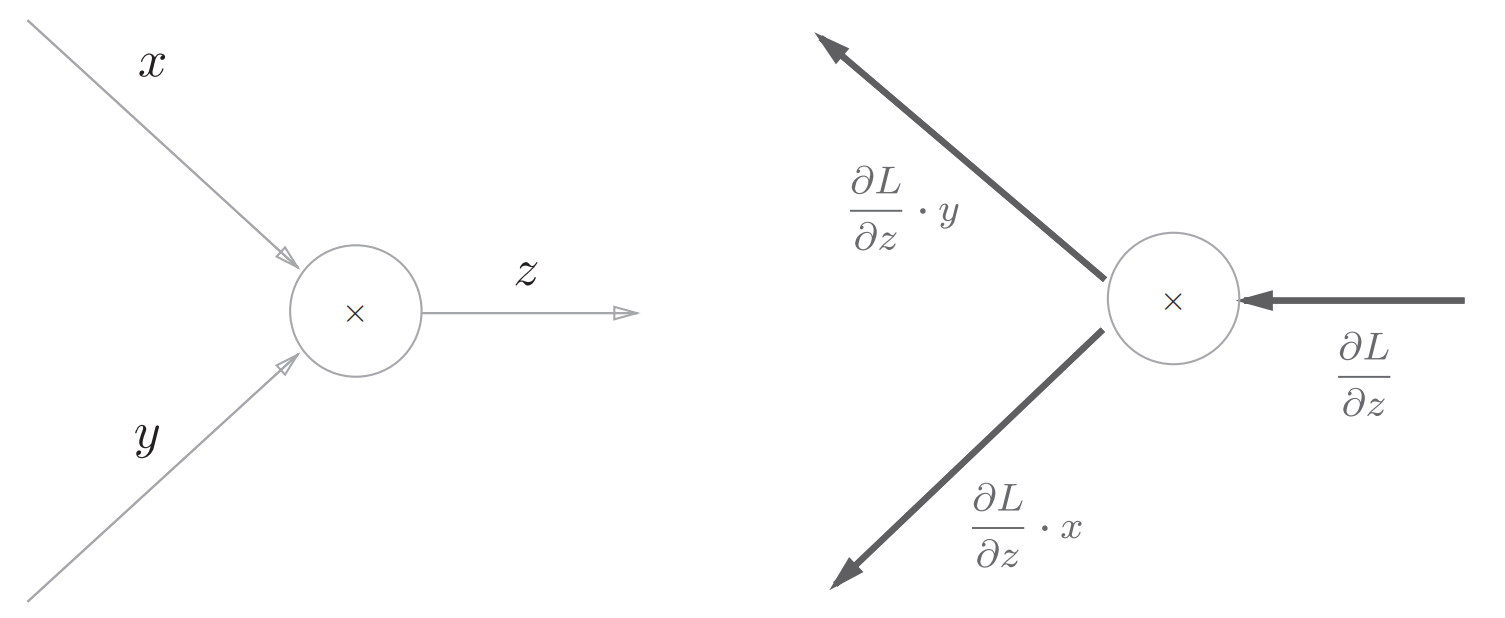
因此乘法的反向传播会乘以输入信号的翻转值,所以在实现乘法的反向传播的时候需要保存正向传播的输入信号
python实现:
###
class MulLayer:
def __init__(self):
self.x = None
self.y = None
def forward(self, x, y):
self.x = x
self.y = y
out = x * y
return out
def backward(self, dout):
dx = dout * self.y # 翻转x和y
dy = dout * self.x
return dx, dy
class AddLayer:
def __init__(self):
pass
def forward(self, x, y):
out = x + y
return out
def backward(self, dout):
dx = dout * 1
dy = dout * 1
return dx, dy
接下来实现激活函数ReLU层和Sigmoid层
ReLU激活函数及其导数:

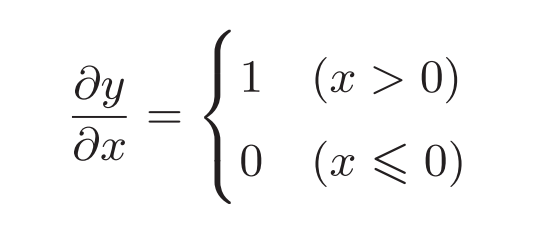
用计算图表示:
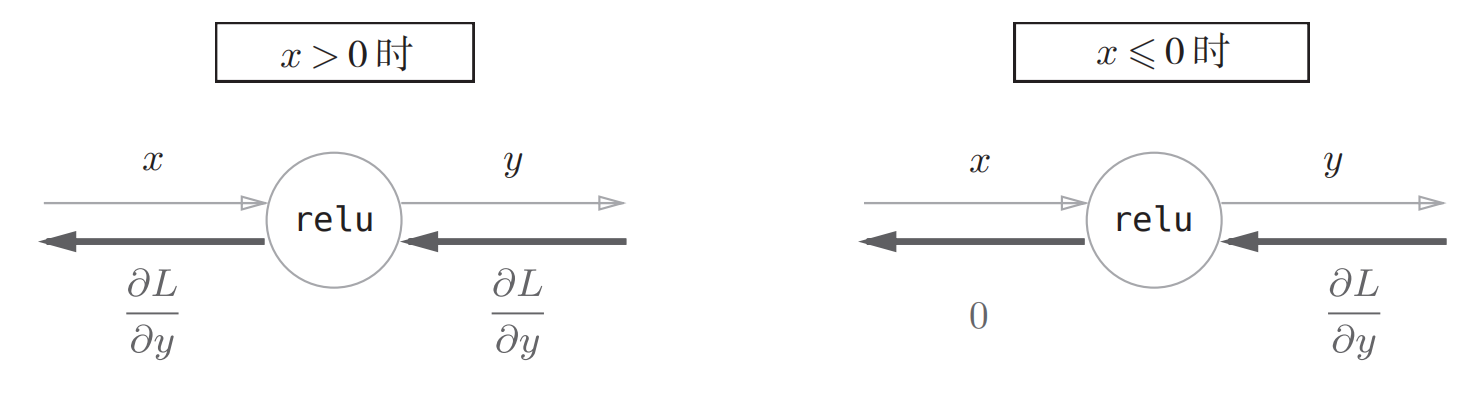
ReLU激活函数就像一个开关,正向传播的时候有电流通过就将开关打开,这个时候反向传播电流就会直接通过;如果正向传播时没有电流就把开关关闭,反向传播时就不会有电流通过
class Relu:
def __init__(self):
self.mask = None
def forward(self, x):
self.mask = (x <= 0)
out = x.copy()
out[self.mask] = 0
return out
def backward(self, dout):
dout[self.mask] = 0
dx = dout
return dx
sigmoid函数为:
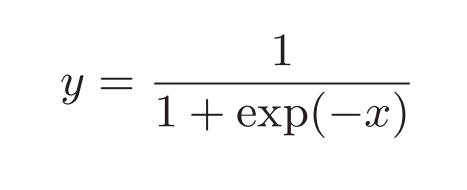
利用计算图表示为:
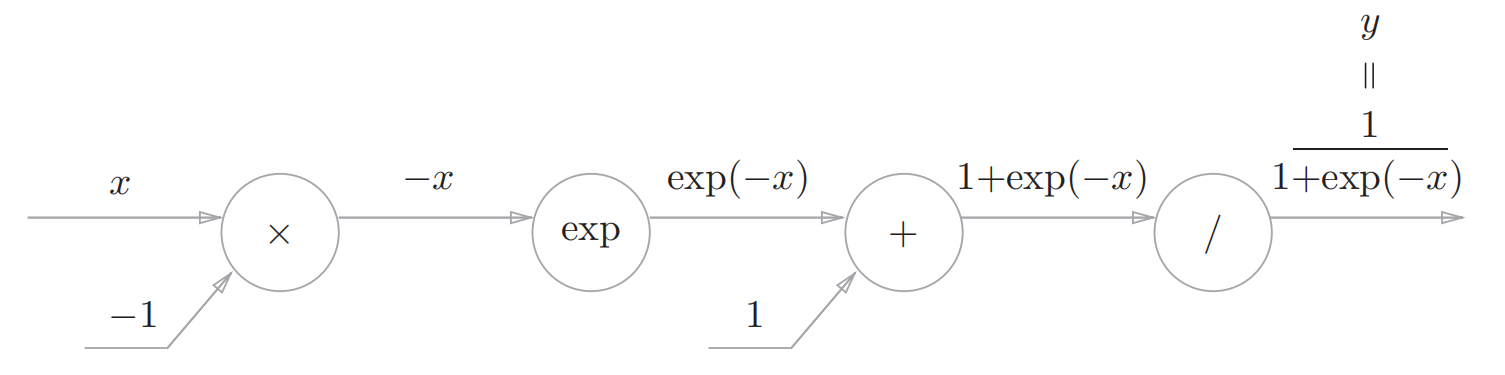
这里面出现了几个新的节点:/和exp节点
/节点表示的函数为:$y=\frac{1}{x}$ ,导数为:
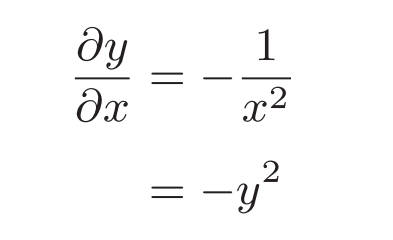
因此该节点将上游的值乘以正向传播的输出平方后再乘以-1传给下游
exp节点表示$y=exp(x)$ 其导数还是其自身:
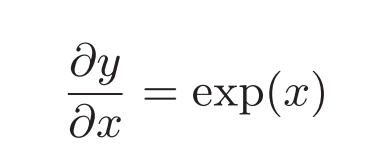
因此exp节点将上游的值乘以正向传播的输出后传给下游
所以结合前面的+和×节点,sigmoid的导数计算图为:
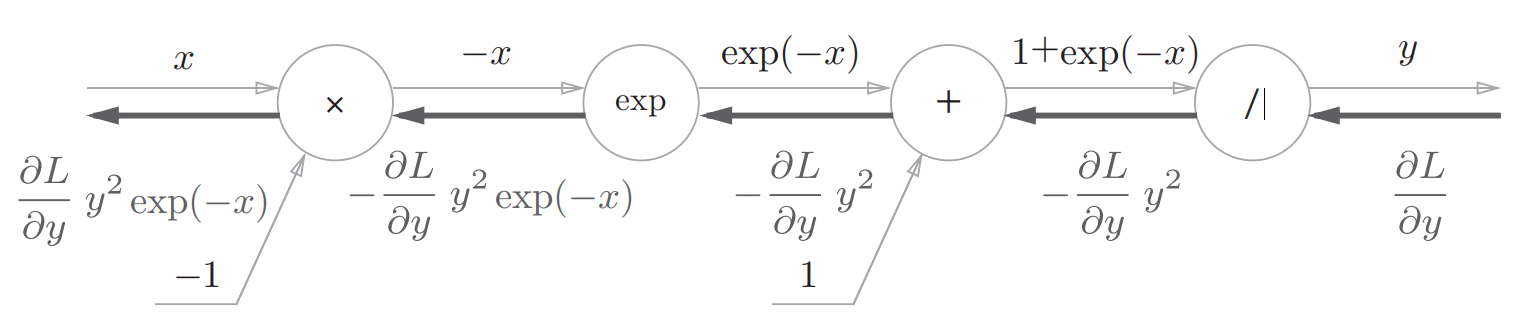
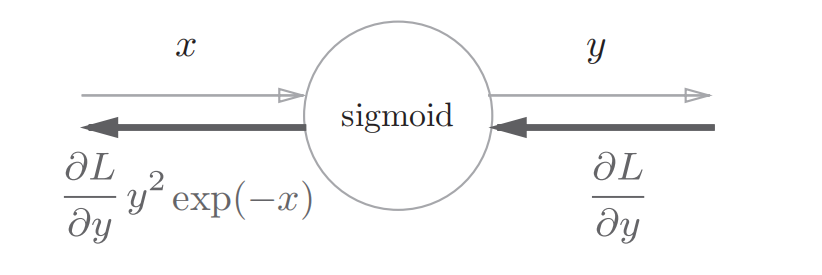
进一步整理得到:
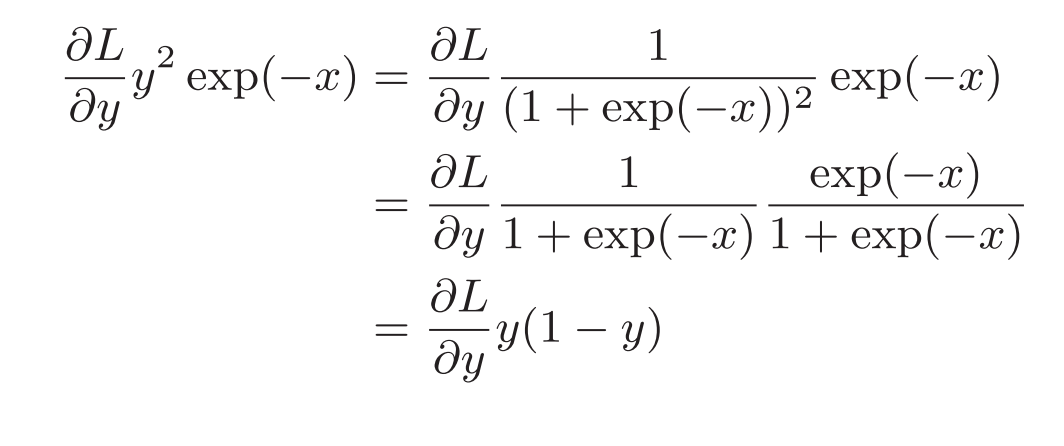
class Sigmoid:
def __init__(self):
self.out = None
def forward(self, x):
out = 1 / (1 + np.exp(-x))
self.out = out
return out
def backward(self, dout):
dx = dout * (1.0 - self.out) * self.out
return dx
对输入信号进行加权求和的层叫做Affine层,可以用如下的计算图来表示:
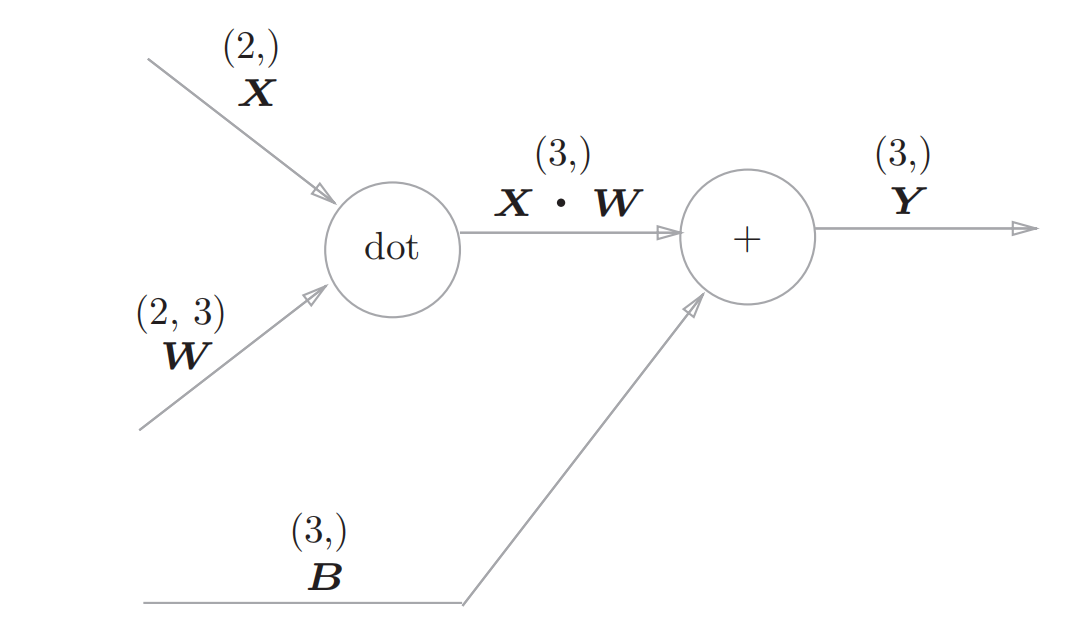
其中dot表示矩阵相乘
其反向传播过程:
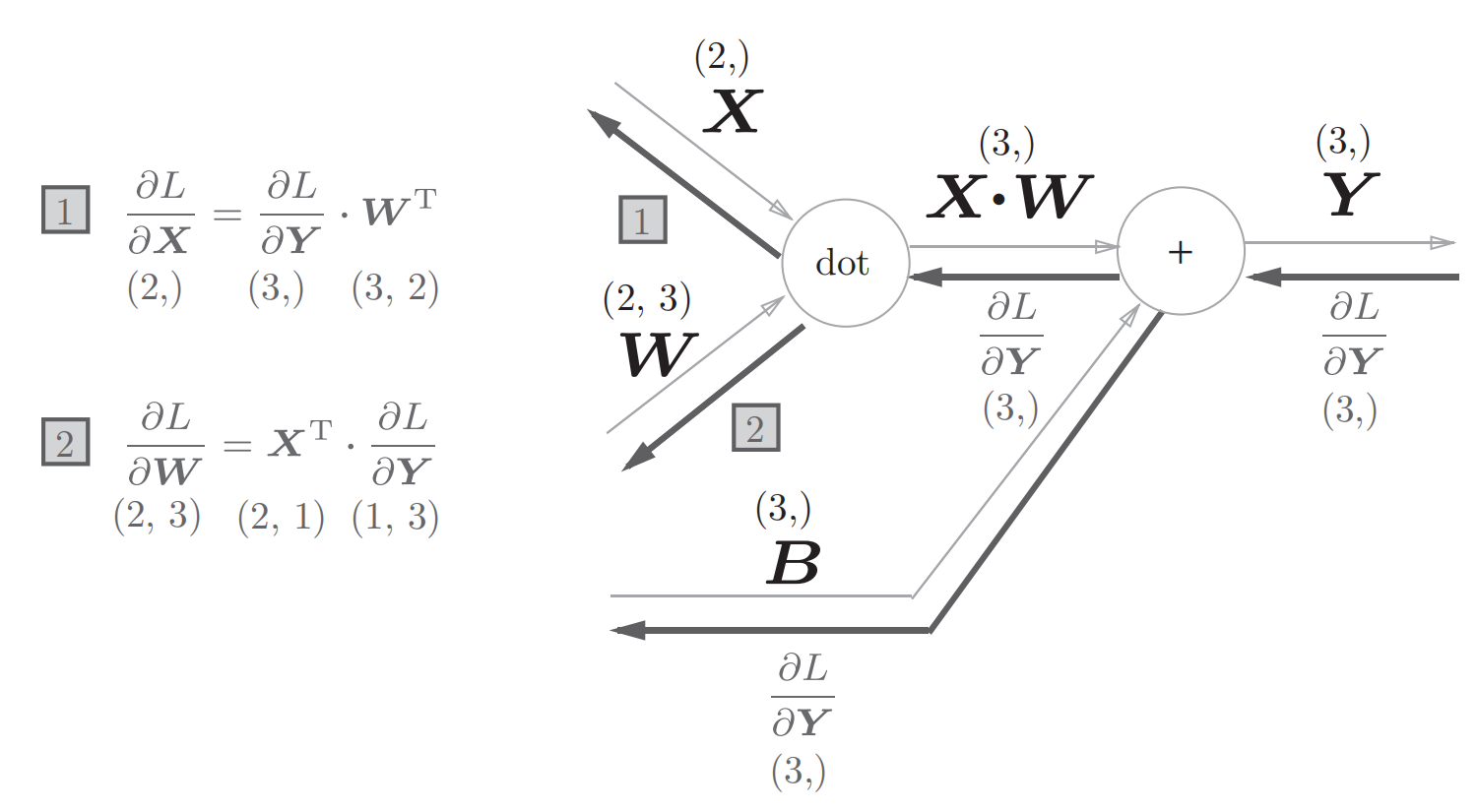
对于1,2可以类比于乘法,再根据矩阵的维度来理解:比如$\frac{\partial (X \cdot W) }{\partial X}$ 如果结果是W,那么W的维度为(2,3)而$\frac{\partial L}{\partial Y}$的维度为(3,1),这样就不能相乘,所以结果是W的转置
基于上面的计算图,可以使用python来实现Affine层:
class Affine:
def __init__(self, W, b):
self.W = W
self.b = b
self.x = None
self.dW = None
self.db = None
def forward(self, x):
self.x = x
out = np.dot(x, self.W) + self.b
return out
def backward(self, dout):
dx = np.dot(dout, self.W.T)
self.dW = np.dot(self.x.T, dout)
self.db = np.sum(dout, axis=0)
return dx
最后还有一个比较重要的是Softmax-with-Loss 层 ,也就是包含Softmax函数和交叉熵误差的层
交叉熵误差表示为:

用计算图表示为:
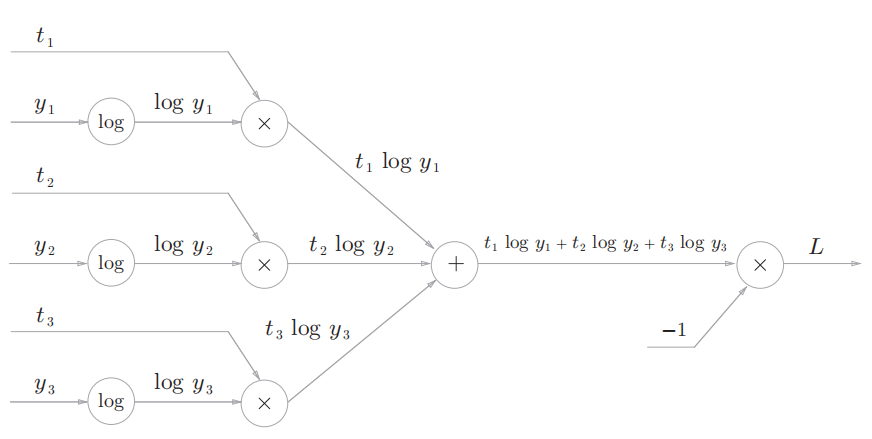
这个反向传播的要注意的就是log节点:
log函数为$y=log(x)$ ,所以其导数为$\frac{\partial y }{\partial x}=\frac{1}{x}$ ,而加节点(原封不动)和乘节点(翻转)之前已经见过了
因此交叉熵误差的反向传播用计算图表示为:
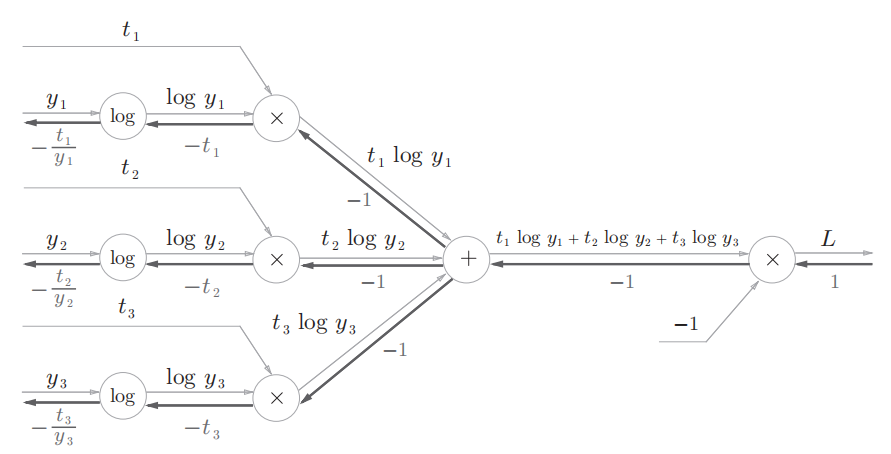
Softmax函数为:
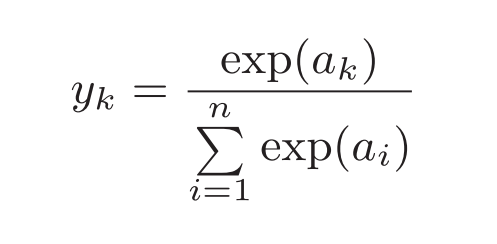
用计算图表示为:
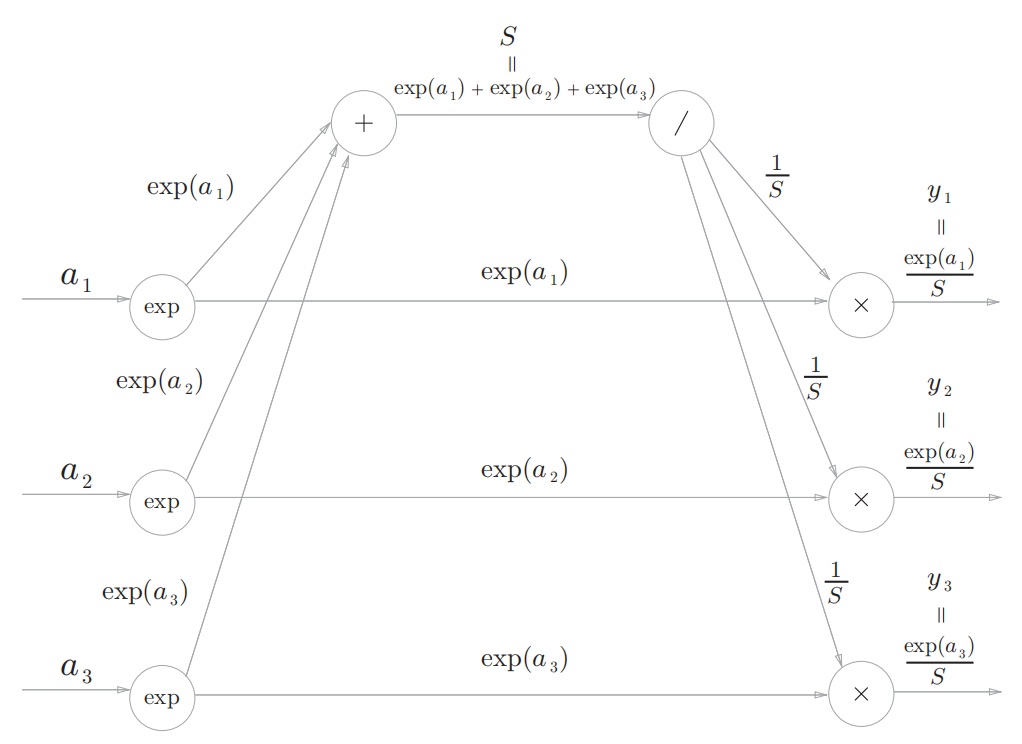
反向传播可以分成几个步骤:
-
交叉熵误差层传过来的值
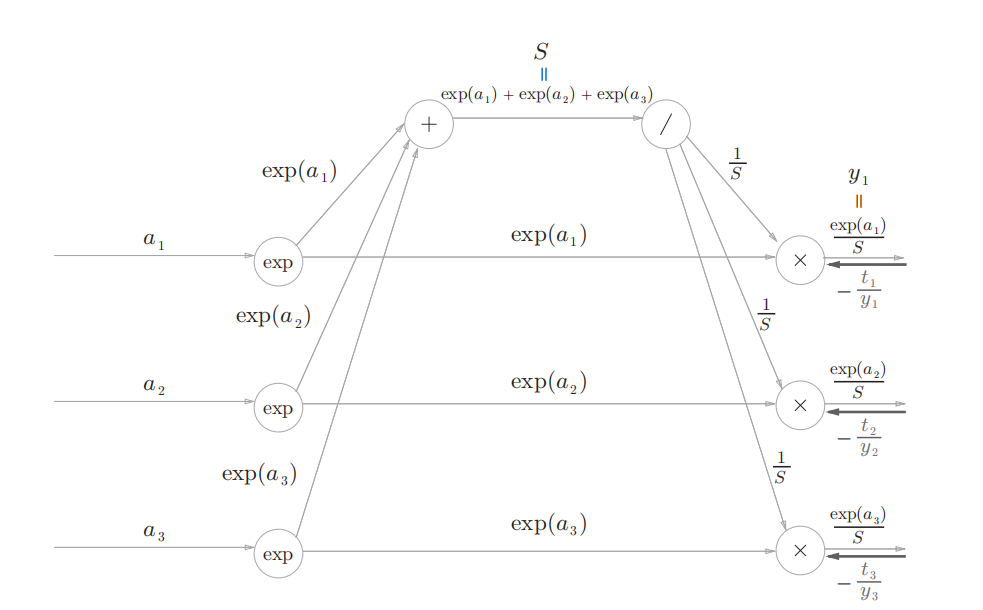
-
乘节点将正向传播的值翻转后相乘:
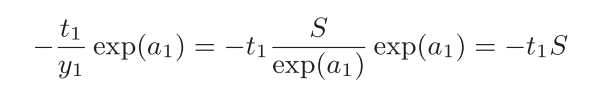
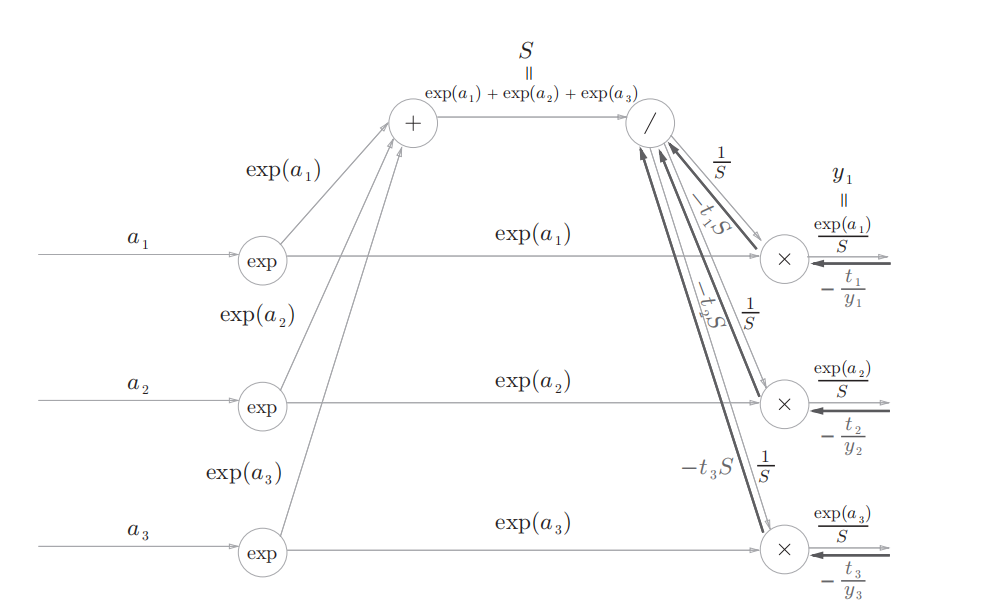
-
正向传播时若有分支流出,则反向传播时它们的反向传播的值会相加,因此对于除节点反向传播的输入为$-S(t_1+t_2+t_3)$ 然后进行除节点的反向传播:$-S(t_1+t_2+t_3)×(\frac{1}{S})^2=\frac{1}{S}(t_1+t_2+t_3)$ ,这里面t表示训练数据的标签为ont-hot向量(0,1向量),因此结果为$\frac{1}{S}$,用计算图表示如下:
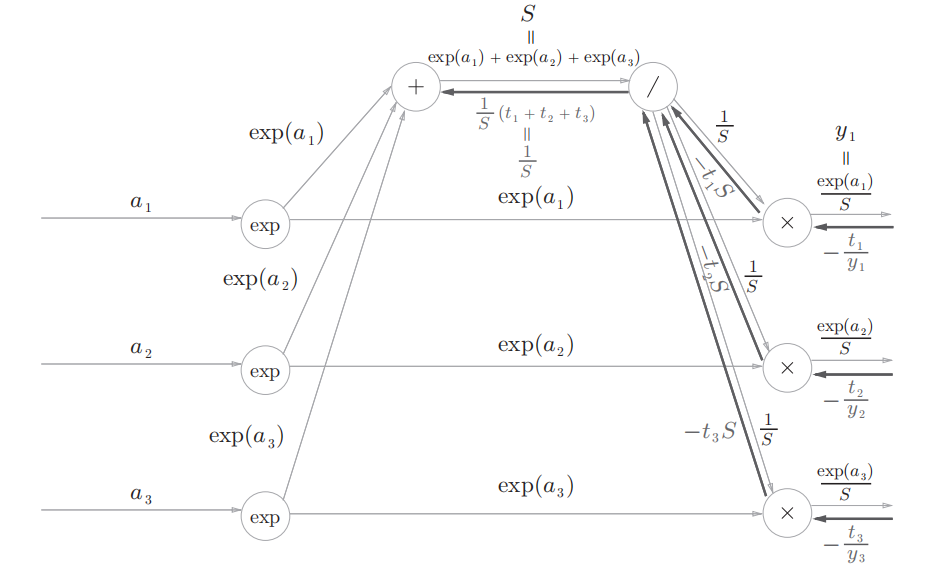
-
加节点原封不动的传递,乘节点进行翻转:
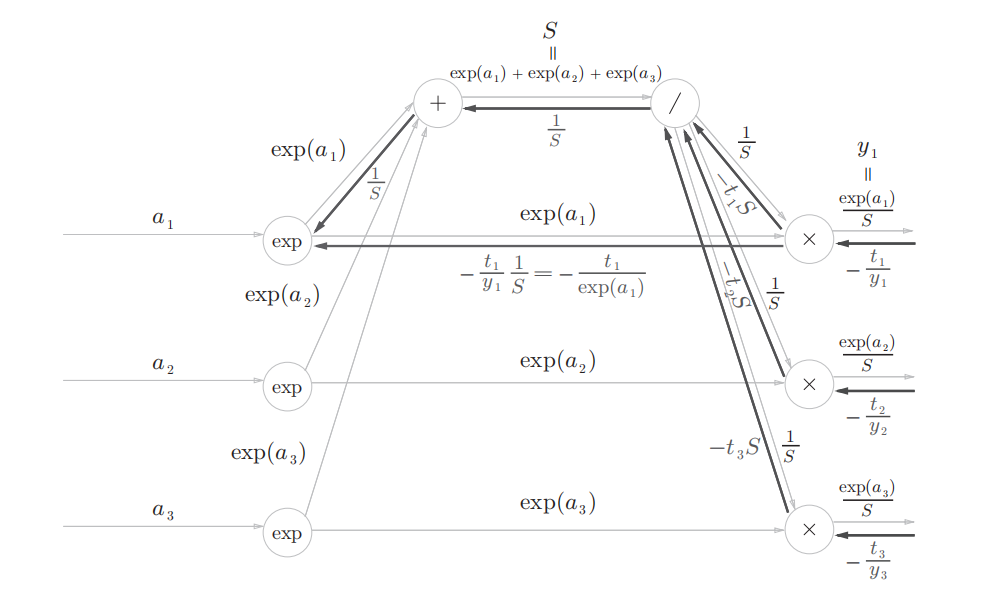
-
exp节点根据前面的推导,将上游的值乘以正向传播的输出后传给下游,也就是$(\frac{1}{S}-\frac{t_1}{exp(a_1)})exp(a_1)$ 整理可得$y_1-t_1$ :

将上面的交叉熵误差和softmax总结起来可以用下面的计算图表示:

这样就可以使用python进行简单的实现:
class SoftmaxWithLoss:
def __init__(self):
self.loss = None # 损失
self.y = None # softmax的输出
self.t = None # 监督数据(one-hot vector)
def forward(self, x, t):
self.t = t
self.y = softmax(x)
self.loss = cross_entropy_error(self.y, self.t)
return self.loss
def backward(self, dout=1):
batch_size = self.t.shape[0]
dx = (self.y - self.t) / batch_size
return dx