线性回归

简单线性回归

简单线性回归假设两个连续变量之间是线性关系的: $Y_i=\beta_0+\beta_1X_i+𝜖_i$ $Y_i$表示第i个因变量(reponse),$X_i$表示第i个自变量(feature),$\beta_0,\beta_1$ 是需要模型的参数,$𝜖_i$是噪音或者说随机误差(random error),在线性回归里面假设$𝜖_i$是服从正态分布: $𝜖$ ~ $norm(0,\sigma^2)$

所以$E(𝜖)=0$ ,上面的式子可以写成： $E(Y_i|X_i)=E(\beta_0+\beta_1X_i+𝜖_i|X_i)=\beta_0+\beta_1X_i$ 线性回归就是估计这个条件期望： $\hat{Y_i}=\hat{\beta_0}+\hat{\beta_1}X_i$ 也就是说我们估计出来的系数解释的是平均的效应：截距𝛽0表示𝑋= 0时的平均响应值,斜率𝛽1表示每增加1个单位，平均响应的增加(即变化率)

基于数据估计的值是$\beta_0+\beta_1X_i$ 而真实的值是$Y_i$ 如何衡量估计值和真实值的接近程度？有很多方法去衡量这个接近度(closeness),但最常用的是最小二乘法

定义残差(residual,e)为真实值和预测值的差,残差平方和( residual sum of squares ,RSS)为所有残差的平方和： $RSS=(Y_1−\hat{β_0}−\hat{β_1}X_1)^2 +(Y_2−\hat{β_0}−\hat{β_1}X_2) +...+(Y_n−\hat{β_0}−\hat{β_1}X_n)$ 最小二乘法就是求出使得RSS最小的$\hat{\beta_0},\hat{\beta_1}$ : $\hat{\beta_1}=\frac{\sum_{i=1}^n(X_i-\bar X)(Y_i-\bar Y)}{\sum_{i=1}^n(X_i-\bar X)} \\ \hat{\beta_0}=\bar{Y}-\hat{\beta_1}\bar X$

使用MASS包中的Boston数据集作为示例：

##linear regression
library(MASS)
library(ISLR)

## data
names(Boston)
# [1] "crim"    "zn"      "indus"   "chas"    "nox"    
# [6] "rm"      "age"     "dis"     "rad"     "tax"    
# [11] "ptratio" "black"   "lstat"   "medv"

##拟合一个简单线性回归模型，自变量是lstat，因变量是medv
lm_fit <- lm(medv~lstat,data = Boston)
summary(lm_fit)

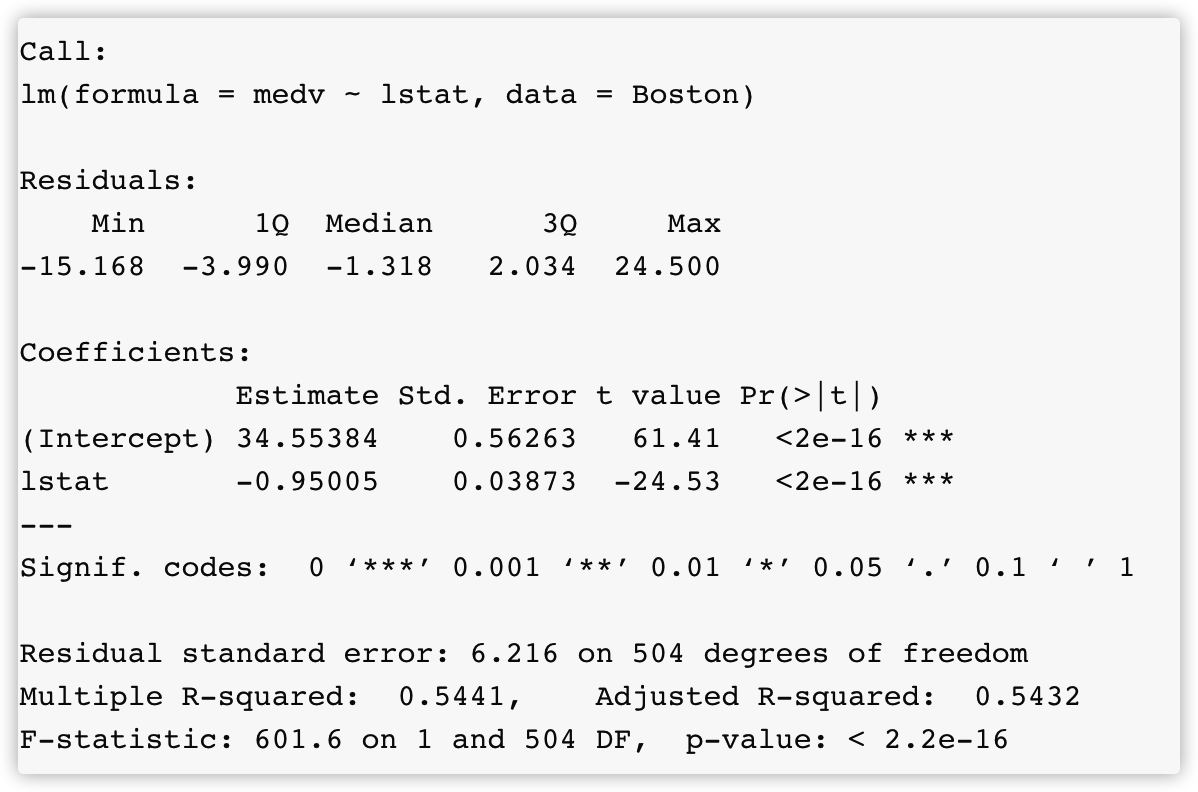
可以使用一些特殊的函数来得到这些信息，比如coef()得到系数

coef(lm_fit)
# (Intercept)       lstat 
# 34.5538409    -0.9500494 

多元线性回归

当自变量有多个的时候就可以使用多元线性回归来拟合数据： $Y = β_0 +β_1X_1 +β_2X_2 +···+β_pX_p+ε$ 系数的估计使用最小二乘法和简单线性回归类似，最小化RSS： $RSS=\sum_{i=1}^n(y_i-\hat{y_i})^2=\sum_{i=1}^n(y_i-\hat{\beta_0}-\hat{\beta_1x_{i1}}-\hat{\beta_2x_{i2}}- ···-\hat{\beta_p}x_{ip})^2$ 可以使用+来加入其它的变量:

lm_fit2 <- lm(medv~lstat+age,data = Boston)
summary(lm_fit2)

如果要加入所有的变量的话，可以使用.来简化操作：

lm_fit_all <- lm(medv~.,data = Boston)
summary(lm_fit_all)

当我们需要向之前的模型中添加变量时可以使用updata函数：

lm_fit3 <- update(lm_fit2,~.+chas)
summary(lm_fit3)

系数估计的准确度衡量

$Y_i=\beta_0+\beta_1X_i+𝜖_i$提供的是对X,Y的真实关系的最好线性度量，通常称为总体回归线(population regression line),而我们基于最小二乘回归估计的$\hat{Y_i}=\hat{\beta_0}+\hat{\beta_1}X_i$相当于对样本数据的线性度量，通常称为最小二乘线(least squares line),也就是说我们想要用这个基于样本计算的值去估计总体的参数

我们知道我们可以用样本的均值去估计总体的均值,并且样本均值是总体均值的无偏估计量（无偏估计量的期望等于要估计的参数）,对于一次抽样，评估利用抽样样本均值去估计总体均值的误差可以使用标准误： $Var(\hat{\mu})=SE(\hat{\mu})^2=\frac{\sigma^2}{n}$ 可以用类似的方法去评估估计的$\hat{\beta_0},\hat{\beta_1}$ 和真实值的差异： $SE(\hat{\beta_0})^2=\sigma^2[\frac{1}{n}+\frac{\bar{X}^2}{\sum_{i=1}^n(X_i-\bar X)^2}],SE(\hat{\beta_1})^2=\frac{\sigma^2}{\sum_{i=1}^n(X_i-\bar X)^2}$ 这里的$\sigma$是前面提到的误差项的方差，也叫残差标准误(RSE),也是需要估计的,估计的方法是最大似然估计： $\hat{\sigma}^2=\frac{1}{n-p-1}\sum_{i=1}^n(Y_i-\hat{Y_i})=\frac{RSS}{n-p-1},p是参数的数量$ 可以通过sigma()函数来获得$\sigma$值(也可以直接看summary里面的Residual standard error)：

sigma(lm_fit)
#[1] 6.21576

有了标准误就可以计算置信区间和进行假设检验了

原假设：X,Y之间没有关系,$\beta_1=0$

备择假设：X,Y之间有关系,$\beta_1\neq0$

检验统计量可以使用t统计量(自由度为n-p-1),进行t检验,得到p值 $t=\frac{\hat{\beta_1}-0}{SE(\hat{\beta_1})}$

参数的t统计量的值(t value)和相应的p值(Pr(>|t|))在模型的summary里面都可以得到

也可以通过confint获得置信区间：

confint(lm_fit)
#                2.5 %     97.5 %
# (Intercept) 33.448457 35.6592247
# lstat       -1.026148 -0.8739505

定性变量的处理

对于一个有两个levels的因子来说，利用其构建回归模型需要创建一个indicator（dummy variable）

以Credit数据为例：因变量是Balance，表示信用卡负债额度

data <- read.csv("~/Downloads/Credit.csv")
colnames(data)
# [1] "Income"    "Limit"     "Rating"    "Cards"     "Age"       "Education"
# [7] "Gender"    "Student"   "Married"   "Ethnicity" "Balance" 

比如我们现在想要看性别间的信用卡负债的差别，可以创建一个dummy 变量： $x_i=\left\{ \begin{aligned} 1\ 男性\\ 0\ 女性 \end{aligned} \right.$ 然后用这个变量去构建回归模型： $y_i=\beta_0+\beta_1x_i+ε_i=\left\{ \begin{aligned} \beta_0+\beta_1+ε_i\ if\ ith\ person\ is\ male\\ \beta_0+ε_i\ if\ ith\ person\ is\ female \end{aligned} \right.$ 所以$\beta_0$就可以解释为女性的平均信用卡负债，$\beta_0+\beta_1$为男性的平均信用卡负债，$\beta_1$就是两者的差

data$Gender <- factor(data$Gender,levels = c("Female","Male"),labels = c(1,0))
lm_fit4 <- lm(Balance~Gender,data = data)

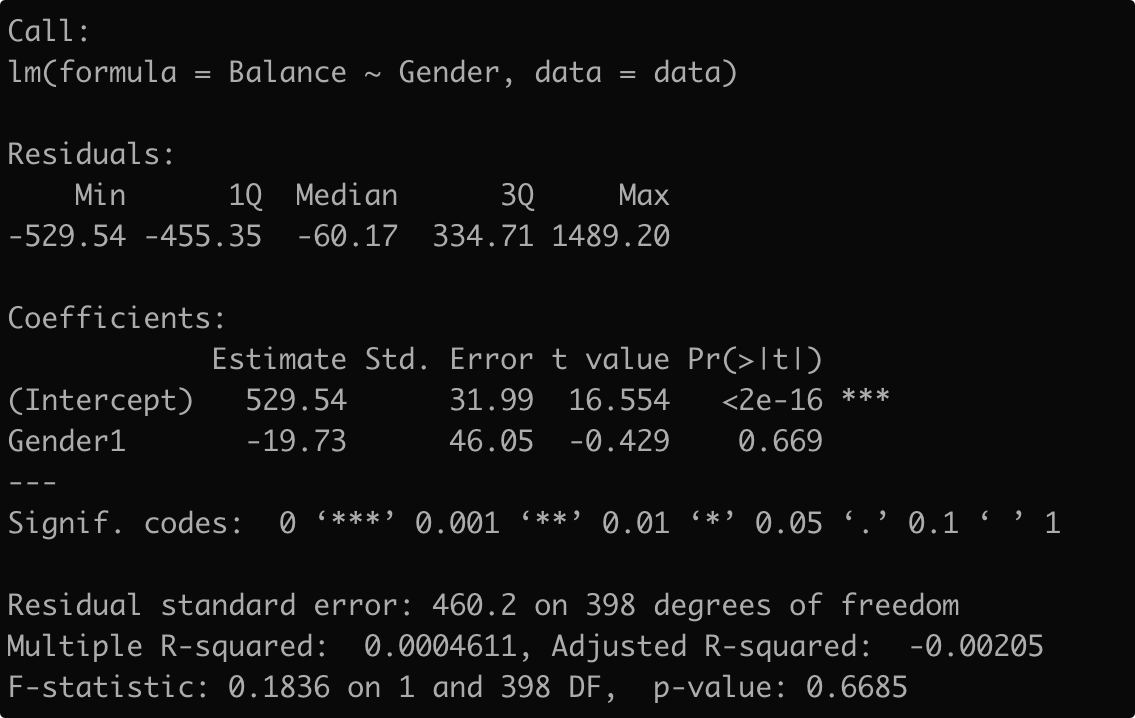
可以看到女性的balance是529.54,而男性的是529.54+(-19.73)=509.80,差值是19.73但是p值比较大，说明没有足够的统计学证据表明性别之间的平均信用卡负债是有差距的

如果定性的预测变量的水平大于两个，我们就不能用一个dummy变量包括这些水平，这个时候我们可以创建额外的dummy变量

比如，我们想要预测信用卡的balance和种族之间的关系，可以创建如下的变量： $x_{i1}=\left\{ \begin{aligned} 1\ if \ ith\ person\ is\ Asian\\ 0\ if \ ith\ person\ is\ not\ Asian \end{aligned} \right.$

\[x_{i1}=\left\{ \begin{aligned} 1\ if \ ith\ person\ is\ Caucasian\\ 0\ if \ ith\ person\ is\ not\ Caucasian \end{aligned} \right.\]

模型可以表示为： $yi = β_0+β_1x_{i1}+β_2x_{i2}+ε_i=\left\{ \begin{aligned} β_0+β_1+ε_i\ if \ ith\ person\ is\ Asian\\ β_0+β_2+ε_i\ if \ ith\ person\ is\ \ Caucasian\\ β_0+ε_i\ if\ ith\ person\ is\ African\ American. \end{aligned} \right.$

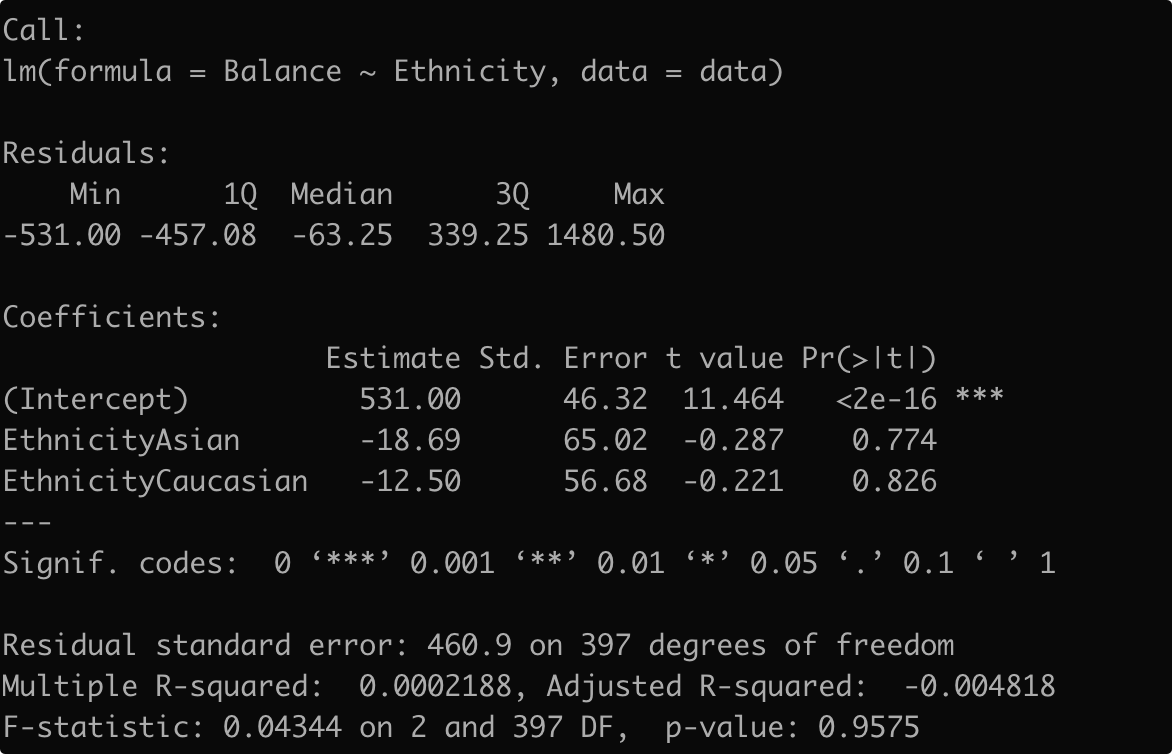
data$Ethnicity <- factor(data$Ethnicity,
                         levels = c("African American","Asian","Caucasian"))
lm_fit5 <- lm(Balance~Ethnicity,data = data)
summary(lm_fit5)

模型的准确度衡量

一旦我们可以拒绝上面的原假设，认为X,Y间有某种关系，下一个问题就是：怎么衡量拟合的模型反映这种关系的程度

在线性回归拟合中一般使用残差标准误(RSE)和R^2^ 来衡量 $RSE=\sqrt{\frac{1}{n-p-1}\sum_{i=1}^n(y_i-\hat{y_i})^2},p是参数的数量$ 可以这样来理解RSE：即使真实的β0，β1已经知道了，根据X来预测Y，平均还会产生RSE个单位的偏离

如果预测的值和实际的值差不多,RSE就比较小;如果预测的远离实际的值,RSE就会比较大

但是由于RSE是一个绝对值,我们不知道多小的RSE表示模型拟合的比较好,在不同的模型间也不好比较,所以我们需要对RSE进行”标准化“

如果没有模型，最朴素的预测就是用均值，所以可以使用均值来代替$\hat{y_i}$来进行标准化 : $NRSE=\frac{\sqrt{\frac{1}{n-p}\sum_{i=1}^n(y_i-\hat{y_i})^2}}{\sqrt{\frac{1}{n-p}\sum_{i=1}^n(y_i-\bar y_i})^2}=\frac{\sum_{i=1}^n(y_i-\hat{y_i})^2}{\sum_{i=1}^n(y_i-\bar y_i)^2}$

\[R^2=1-NRSE=1-\frac{\sum_{i=1}^n(y_i-\hat{y_i})^2}{\sum_{i=1}^n(y_i-\bar y_i)^2}\]

当$R^2$小于0，说明用模型还不如没有模型(直接用平均值预测)

可以对$R^2$变换一个形式： $R^2=\frac{\sum_{i=1}^n(y_i-\bar{y_i})^2-\sum_{i=1}^n(y_i-\hat{y_i})^2}{\sum_{i=1}^n(y_i-\bar y_i)^2}=\frac{TSS-RSS}{TSS}$

TSS(total sum of squres)衡量的是Y的总的变化，RSS表示拟合模型后Y的变化仍然不能被X的变化解释的部分

因此R^2^ 表示的是通过建立模型，Y的变化可以被X解释的比例

上面的例子就说明住房价格的变化的74%可以被这13个变量解释

当加入变量时RSS是单调递减,R^2^是单调递增,如果使用这些标准选择的最优模型肯定是含有较多变量的;并且这这些方法衡量的是训练集的误差，而我们更希望得到的是有着更低的测试集误差的模型，所以在比较多个有着不同自变量数目的模型的时候这些方法就不适用了

其他的方法：AIC(Akaike information criterion) ;BIC(Bayesian information criterion) ;矫正的R^2^, $C_p$ $C_p=\frac{1}{n}(RSS+2d\hat{\sigma}^2)$ d表示变量的数量，相当于在RSS上加了一个罚分项($2d\hat{\sigma}^2$),可以证明$C_P$是测试误差的无偏估计，所以最佳的模型$C_p$是最低的 $AIC=\frac{1}{n\hat{\sigma}^2}(RSS+2d\hat{\sigma}^2)$ AIC和$C_p$是成比例的 $BIC=\frac{1}{n\hat{\sigma}^2}(RSS+log(n)d\hat{\sigma}^2)$ 因为当n大于7的时候log(n)是大于2的，所以BIC对更多的变量给予相对于$C_p$较多的罚分，结果就是相对于$C_p$会选择更小的模型 $adjusted\ R^2=1-\frac{RSS/(n-d-1)}{TSS/(n-1)}$ 当变量增多的时候RSS会下降，但是$\frac{RSS}{n-d-1}$ 下降还是上升与RSS和d相关，当RSS下降比较多的时候adjusted R^2^就会上升，所以最佳的模型是矫正的R^2^最大的模型

这几种方法都是对测试集误差的估计,并且基于一些假设(误差项服从正态分布等)，另外一个选择就是使用交叉验证的方法直接来计算测试误差(将数据分成训练集和测试集，在训练集里面拟合模型，选择模型；在测试集里面估计测试误差)

多自变量系数复合假设检验

前面是对单个系数的检验，但是我们建立一个模型最开始的问题就是选择的变量中是不是至少有一个变量和Y是相关的

所以现在的原假设为：所有的变量都与Y无关，$\beta_1=\beta_2=…=\beta_p=0$; 备择假设为：至少有一个变量与Y相关，也就是至少有一个$\beta_j$不为0

检验的统计量为F统计量： $F=\frac{(TSS-RSS)/p}{RSS/(n-p-1)},p是变量的数目$ 自由度是p,n-p-1

注意：当定性变量有多个水平的时候，单独看每个水平的t检验显著性不能说明变量的显著性，因为定性变量的显著性意味着各个水平对因变量影响的差异

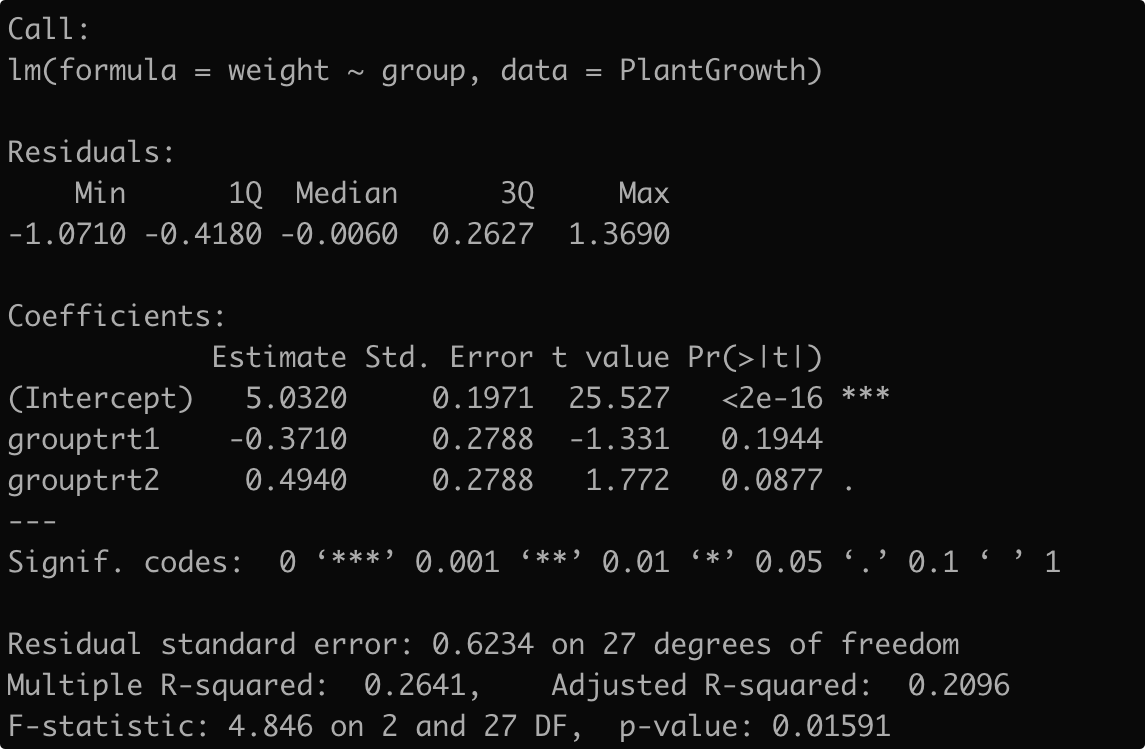
以R中的数据集PlantGrowth为例，因变量是weight(植物的干重)，自变量是group有3个水平，两个实验组(trt1,trt2)一个对照组(ctrl1)

a <- lm(weight~group,data = PlantGrowth)
summary(a)
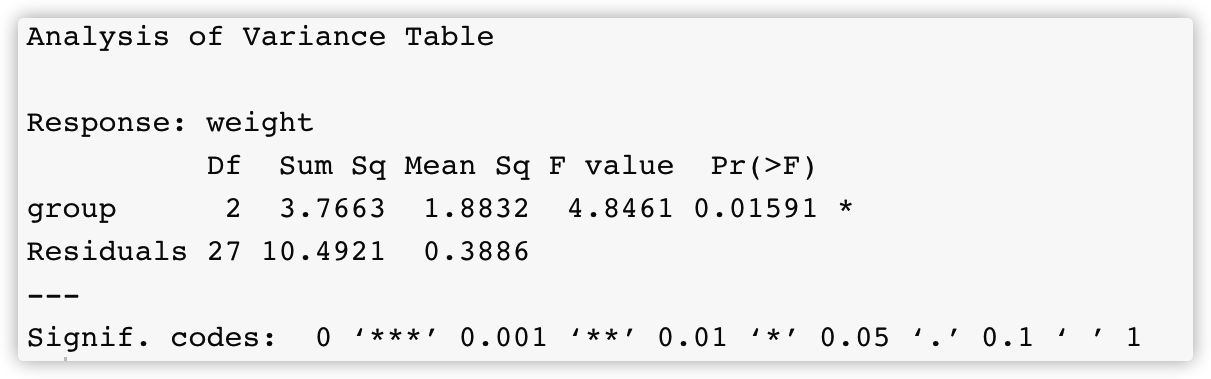
##或者用anova方差分析
anova(a)

变量选择

决定哪些自变量与因变量相关，从而构建一个包含这些变量的模型的过程叫做变量选择(variable selection)，最直观的方法就是列出所有可能的模型看哪个最好

最常用的3种经典的方法有：

best subset
Forward selection
Backward selection
Mixed selection

Best subset

算法：

$M_0$表示空模型，即没有任何自变量
对于k=1,2,…p:
- 拟合含有k个自变量的所有模型，$\binom{p}{k}$个
- 在$\binom{p}{k}$个模型中选择一个最优的模型$M_k$(最小的RSS或者最大的R^2^)
在$M_0,M_1,M_2,…M_k$的p+1个模型中选择一个最优的模型,注意这个时候不能使用RSS或者R^2^ ,因为当加入变量时RSS是单调递减,R^2^是单调递增, 所以如果使用这些标准选择的最优模型肯定是含有所有变量的，因此使用交叉验证的方法，或者BIC AIC或者矫正的R^2^

需要考虑2^p^个模型，计算量比较大

使用的数据是ISLR包里面的Hitters数据，根据一些变量(一共有19个变量)来预测棒球运动员的工资(Salary)：

library(ISLR)
Hitters <- na.omit(Hitters)
names(Hitters) 
# [1] "AtBat"     "Hits"      "HmRun"     "Runs"      "RBI"      
# [6] "Walks"     "Years"     "CAtBat"    "CHits"     "CHmRun"   
# [11] "CRuns"     "CRBI"      "CWalks"    "League"    "Division" 
# [16] "PutOuts"   "Assists"   "Errors"    "Salary"    "NewLeague"

leaps包的regsubsets函数可以来进行best subset selection:

library(leaps)
fit_full <- regsubsets(Salary~.,data = Hitters)
summary(fit_full)

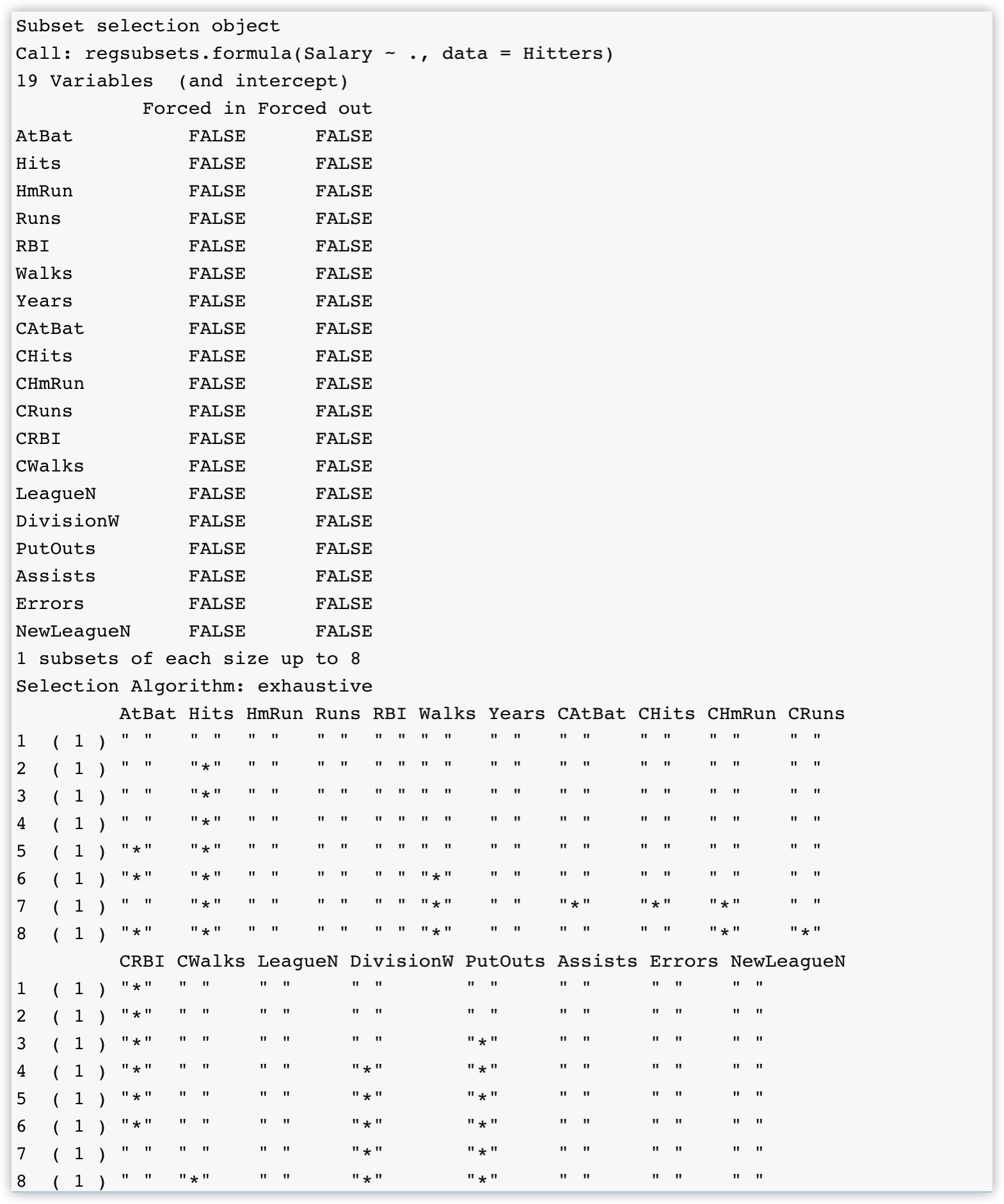
标星号的表示在相应变量数量的模型中选择的变量，默认只输出最好的8个，使用nvmax参数指定输出的模型数量

fit_full <- regsubsets(Salary~.,data = Hitters,nvmax = 19)
summary(fit_full)

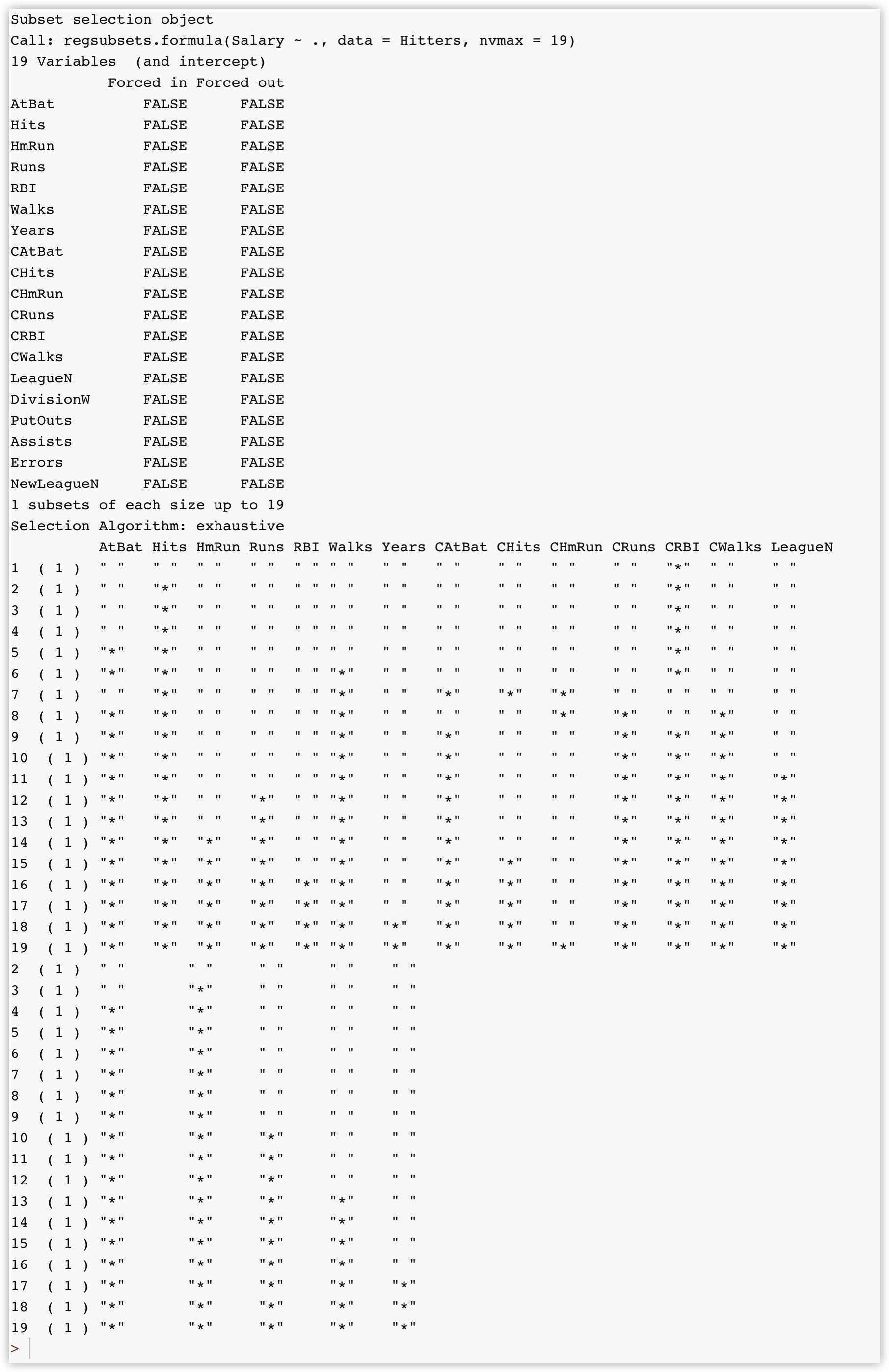
summary也会返回R^2^,AIC BIC 矫正的R^2^, $C_p$ ：

summ <- summary(fit_full)
names(summ)
#[1] "which"  "rsq"    "rss"    "adjr2"  "cp"     "bic"    "outmat" "obj" 
summ$rsq
# [1] 0.3214501 0.4252237 0.4514294 0.4754067 0.4908036 0.5087146 0.5141227 0.5285569 0.5346124
# [10] 0.5404950 0.5426153 0.5436302 0.5444570 0.5452164 0.5454692 0.5457656 0.5459518 0.5460945
# [19] 0.5461159

par(mfrow=c(2,2))
plot(summ$rss ,xlab="Number of Variables ",ylab="RSS",
     type="l")
plot(summ$adjr2 ,xlab="Number of Variables ",
     ylab="Adjusted RSq",type="l")
which.max(summ$adjr2)
points(11,summ$adjr2[11], col="red",cex=2,pch=20)
plot(summ$cp ,xlab="Number of Variables ",ylab="Cp", type='l')
which.min(summ$cp ) #[1] 10
points(10,summ$cp [10],col="red",cex=2,pch=20)
which.min(summ$bic )#[1] 6
plot(summ$bic ,xlab="Number of Variables ",ylab="BIC",
       type='l')
points(6,summ$bic [6],col="red",cex=2,pch=20)

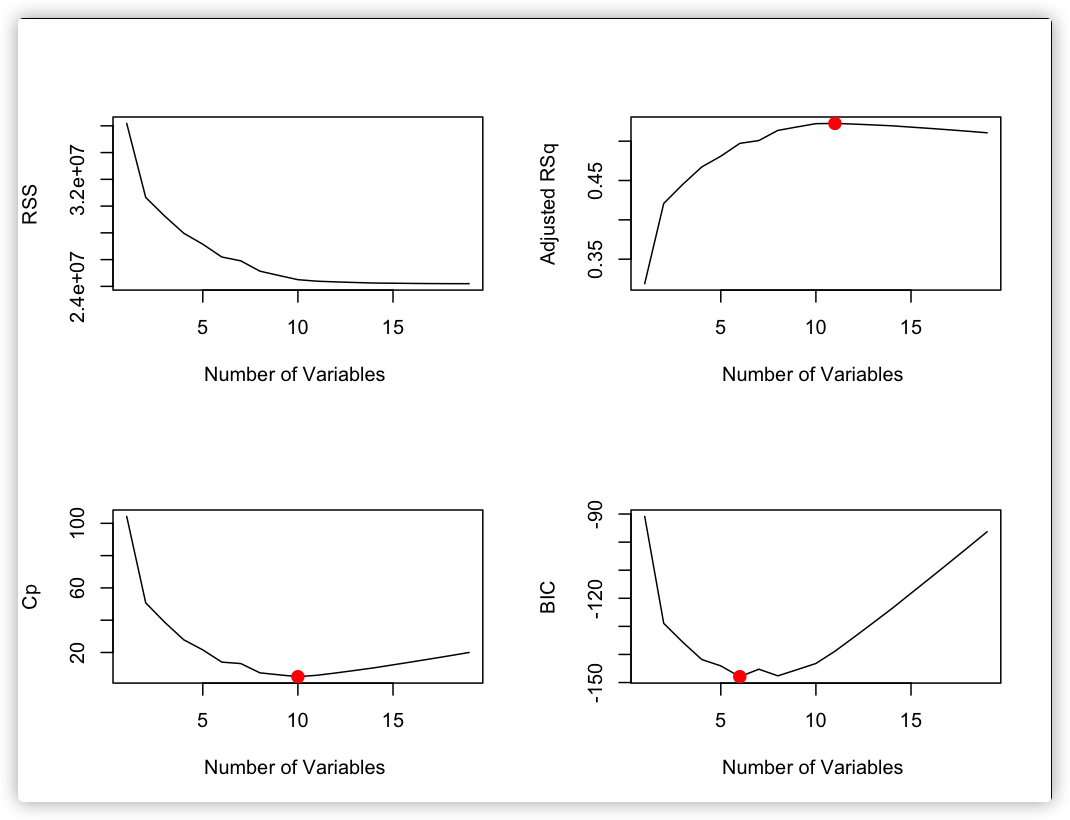
选择模型：

coef(fit_full ,6)
# (Intercept)     AtBat        Hits     Walks         CRBI        DivisionW      PutOuts 
# 91.5117981   -1.8685892   7.6043976    3.6976468    0.6430169 -122.9515338    0.2643076 

Forward selection

算法：

$M_0$表示空模型
对于k=0,…p-1
- 拟合所有在原来模型上加上一个变量的模型，p-k个
- 在p-k个模型中选择一个最优的模型(最小的RSS或者最大的R^2^)
在$M_0,…M_p$中使用交叉验证或者AIC BIC或矫正的R^2^选择最优的模型

需要考虑$1+p(p+1)/2$个模型，缺点就是每个模型都必须包含上一个变量，比如有3个变量，最佳的模型是包含$X_2和X_3$ 但是这种方法就找不到这种模型

使用参数methods="forward"来进行Forward selection

fit_forward <- regsubsets(Salary~.,data = Hitters,method = "forward",nvmax=19)
summary(fit_forward)

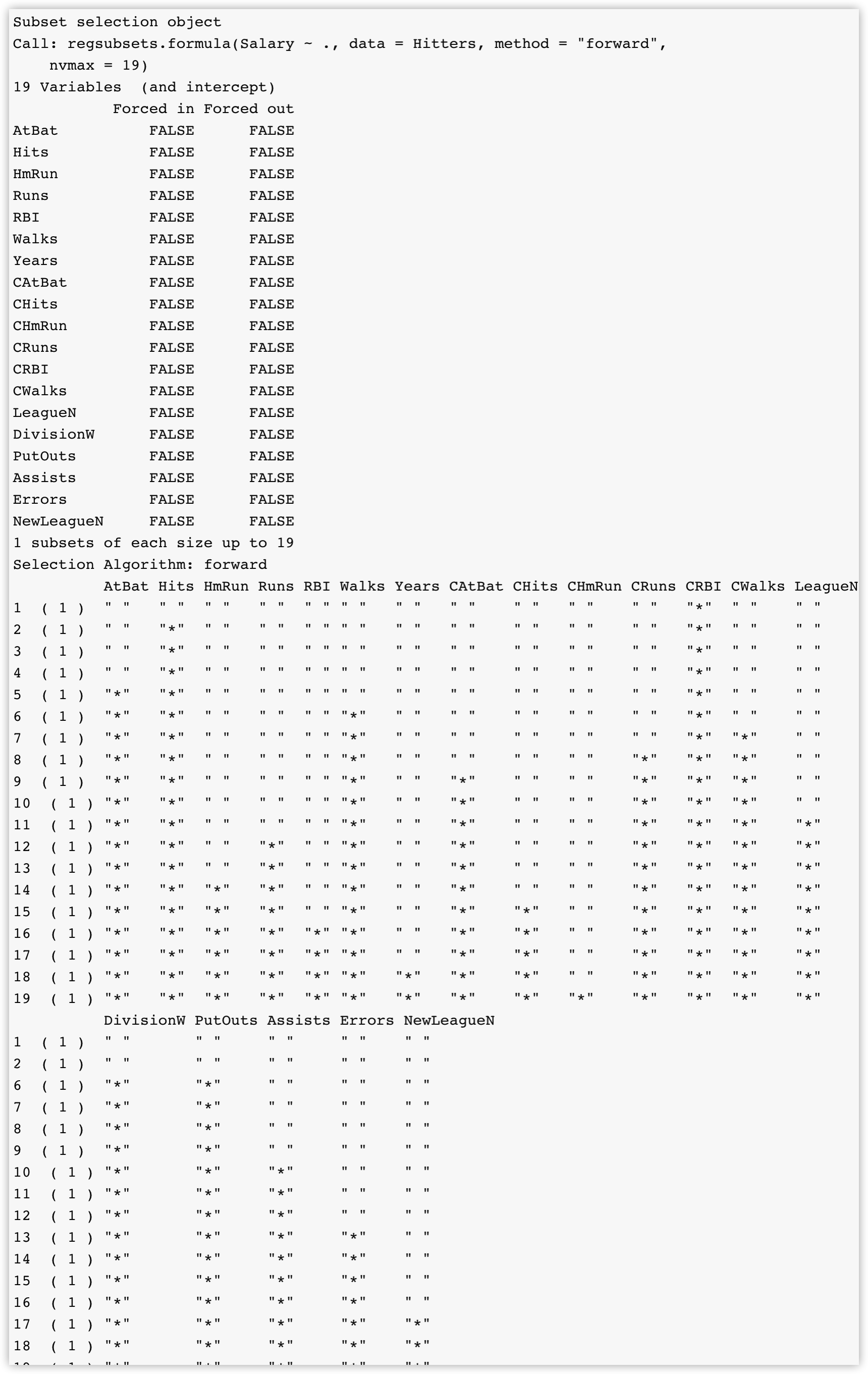
可以看到最好的一变量模型包含CRBI后面的模型都必须有CRBI这个变量

Backward selection

算法：

$M_p$表示全模型，含有全部的变量
对于k=p,p-1,…1
- 拟合所有在原来模型上减去一个变量的模型，k个
- 在k个模型中选择一个最优的模型(最小的RSS或者最大的R^2^)
在$M_0,…M_p$中使用交叉验证，或者AIC BIC或矫正的R^2^选择最优的模型

需要考虑$1+p(p+1)/2$个模型

使用methods=backward来进行Backward selection

其他问题

互作项

有些时候不同的变量间会有相互作用，例如：基于生产线和工人的数量来预测产品的产量，这里面工人的数量和生产线的数量是有相互作用的，如果工人的数量不足，生产线再多也不能增加产量

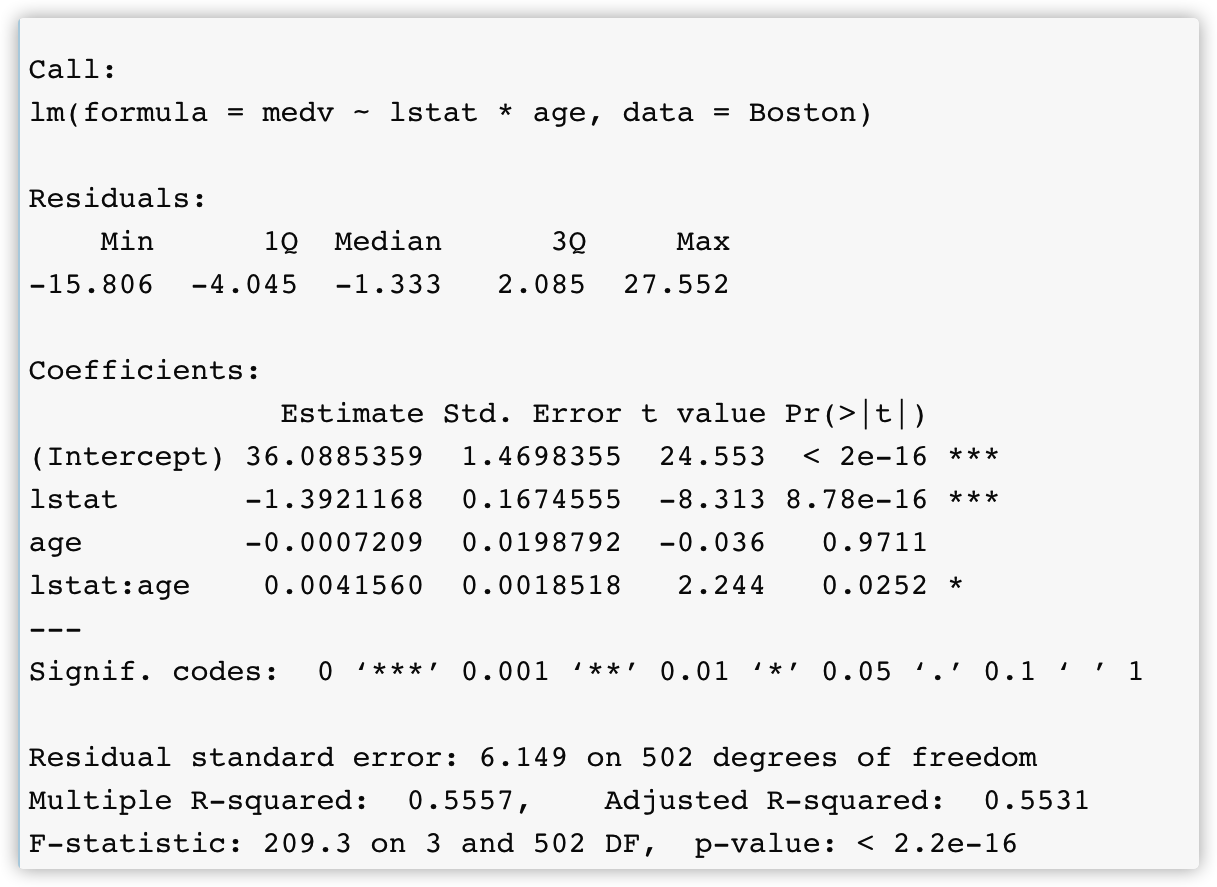
可以在模型中加入互作项(interaction term): $Y=\beta_0+\beta_1X_1+...\beta_iX_iX_j+...+𝜖$

summary(lm(medv~lstat*age,data = Boston))

非线性关系

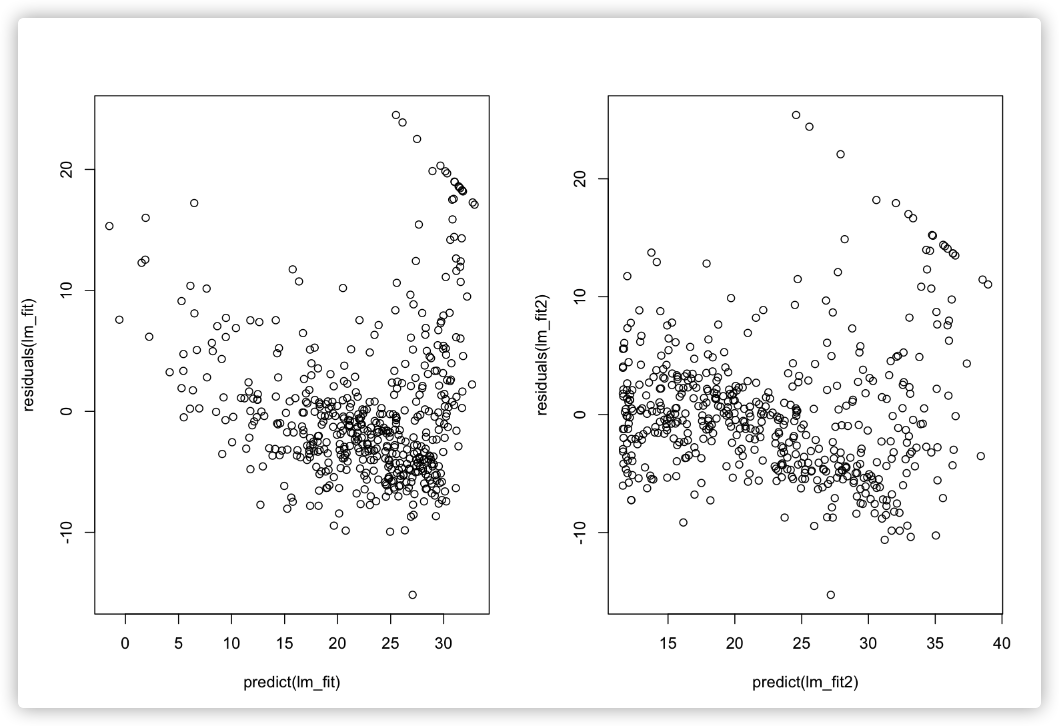
可以用残差图(残差和预测值画散点图)来识别数据的非线性关系

lm_fit <- lm(medv~lstat,data=Boston)
par(mfrow=c(1,2))
plot(lm_fit)
plot(predict(lm_fit),residuals(lm_fit))
lm_fit2=lm(medv~lstat+I(lstat^2),data = Boston)
plot(predict(lm_fit2),residuals(lm_fit2))

误差项的一些假设

之前对估计的回归系数算出来的标准误是假设误差项ε是相互独立的，不相关的，但是如果这些误差项不是独立的那么我们算的方差变小，标准误变小，相应的系数的t统计量就会变大，所以置信区间会变窄，p值就会比真实的要低，导致错误的结论

比如我们基于体重去预测身高，如果这个数据集中有一些个体来自同一个家庭，或者饮食类似，那么误差项独立的假设就不能成立，所以一个良好的实验设计对模型的建立是非常重要的

线性回归模型另一个重要的假设是误差项有着不变的方差$Var(\epsilon_i)=\sigma^2$ ，但是有些时候这个假设不成立，我们可以通过Residual plots的模式来简单判断，如下左图，当response的值变大的时候残差的波动范围也变大(呈喇叭形)，这个时候可以认为方差不齐，右图是经过log转化的：

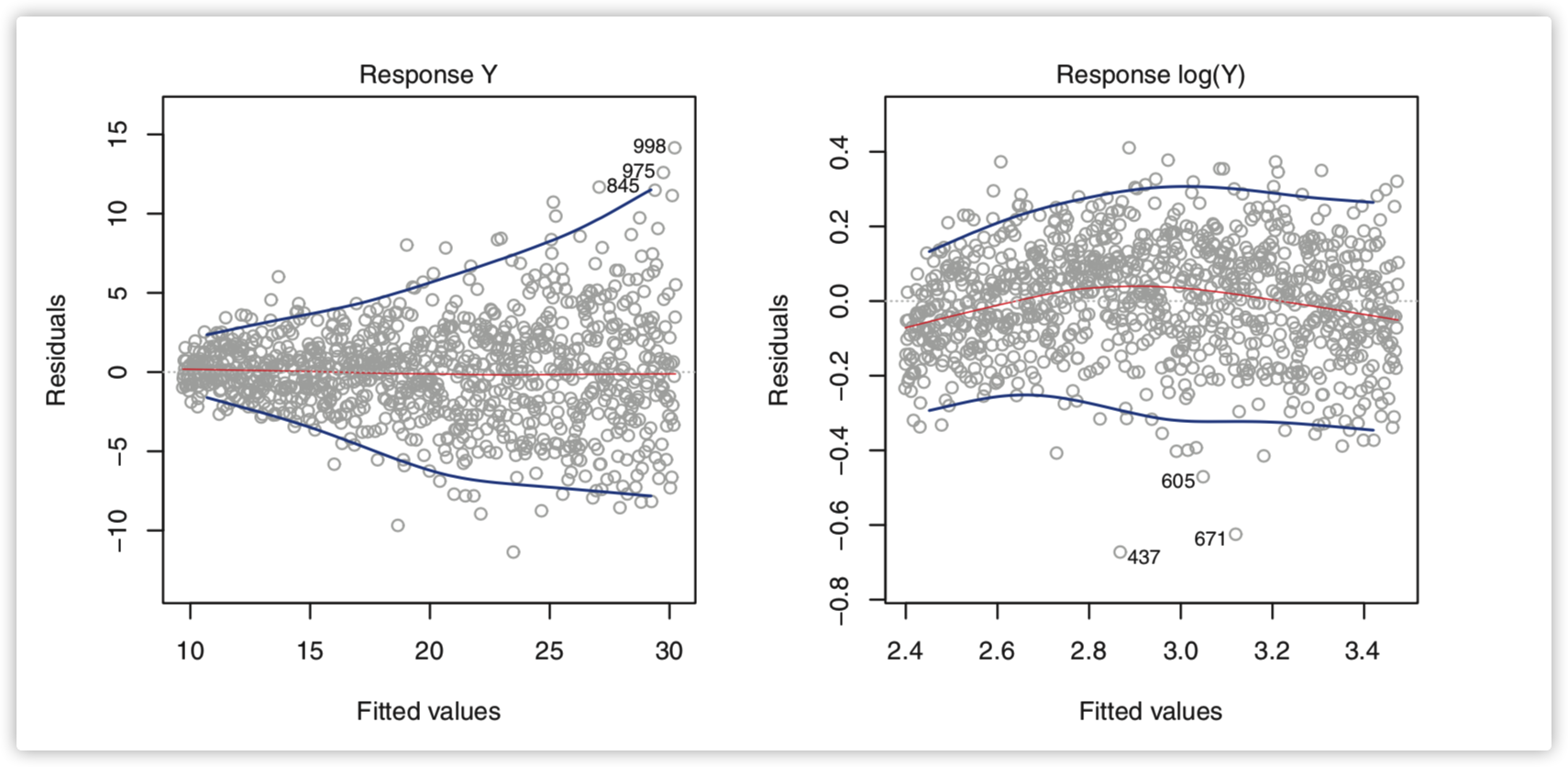
共线性

Collinearity(共线性)指的是两个或者多个变量间紧密相关

判断共线性的一个方法就是计算VIF(variance inflation factor) $Y = β_0 +β_1X_1 +β_2X_2 +···+β_pX_p+ε$ 对每个$X_i$都可以计算VIF

对于$X_i$,将$X_i$视为因变量，与其他的自变量进行最小二次线性回归拟合可以计算出$R_i^2$
计算VIF： $VIF=\frac{1}{1-R_i^2}$ VIF在5-10之间认为是中度共线性，大于10共线性很严重

对于共线性可以有两种解决方法：丢弃共线性的变量中的一个；或者将共线性的变量结合成一个变量